Метод пространственной выборки
Менее распространен, чем метод временных рядов. Построение модели начинается с оценки чувствительности ценных бумаг к определенным факторам. Затем для некоторого периода времени оцениваются значения этих факторов на основе анализа доходностей ценных бумаг и их чувствительности к факторам. Этот процесс повторяется для большого числа временных интервалов, что позволяет дать оценки для стандартных отклонений факторов и их корреляций.
Однофакторные модели В методe пространственных выборок используются данные по различным типам акций для одного момента времени, в то время как для временных рядов строят модель по одному типу акций для различных моментов времени. На рисунке приведен гипотетический пример связи между доходностями акций нескольких типов за определенный период времени и одним из атрибутов ценных бумаг - ставкой дивиденда – для каждого типа акций. Каждая точка относится к одному определенному типу акций, показывая их доходность и ставку дивиденда в рассматриваемом временном интервале. В этом примере акции с более высокой ставкой дивиденда имеют тенденцию к более высокой доходности, чем акции с низкой ставкой дивиденда.
Метод пространственной выборки использует чувствительности для оценки значений факторов. Поэтому такие факторы называются эмпирическими. В методе временных рядов, напротив, известные значения факторов используются для получения оценок чувствительности ценных бумаг. Такие факторы называютсяфундаментальными. 2.3.3 Факторный анализ
В рамках факторно-аналитического метода построения факторной модели неизвестны ни значения факторов, ни чувствительности ценных бумаг к этим факторам. Для определения числа факторов и чувствительностей к данным о доходностях ценных бумаг в прошлом просто применяется статистический метод, называемый факторным анализом. При использовании этого метода доходности некоторой выборки ценных бумаг рассматриваются за большое число временных периодов в целях установления одного или нескольких статистически значимых факторов, которые могли бы привести к ковариации доходностей, наблюдаемых в этой выборке.
Ограничения 1) Риски и доходности, связанные с разными факторами, а также чувствительности ценных бумаг к факторам могут меняться с течением времени. 2) Факторная модель не является равновесной моделью формирования цен на финансовые активы. Сравним, например, ожидаемую доходность акций согласно однофакторной модели с ожидаемой доходностью в модели САРМ:
Оба уравнения показывают, что ожидаемая доходность акций связана с некоторой характеристикой этих акций, bi или bi. Если обе величины изменяются в одном направлении, то они одинаково влияют на ожидаемую доходность ценных бумаг, поэтому между формулами ожидаемой доходности не видно заметных различий. В этом отношении ключевым является другой член правой части каждого из равенств: ai и rf. Значение rf. в САРМ одинаково для всех видов акций. В факторной модели величина ai меняется от одного типа акций к другому, поэтому модель не равновесная. Если равновесие имеет место, то факторная модель и САРМ связаны следующими соотношениями. Пусть фактические доходности генерируются однофакторной моделью, в которой фактор F является доходностью рыночного портфеля rМ, тогда ожидаемые доходности будут равны (так как
Перепишем уравнение
Отсюда видно, что параметры однофакторной модели и модели САРМ должны быть связаны между собой следующим образом:
Задачи.
1. Рассмотрим в рамках однофакторной модели ценную бумагу со значением нулевого фактора 4% и чувствительностью к фактору, равной 0,50. Пусть значение фактора равно 10%. При этом доходность ценной бумаги составляет 11%. Какая часть доходности связана с нефакторными элементами? Решение. rt = a + bFt + et= 4+0,5×10 + et= 11, откуда et= 2. 2/11=0,18 или 18%.
2. В рамках однофакторной модели рассмотрим портфель из двух ценных бумаг со следующими характеристиками:
А) Если стандартное отклонение фактора равно 15%, то чему равен факторный риск Б) Ответьте на вопросы пункта А, предположив, что часть портфеля инвестирована в безрисковый актив и что доля инвестирования в безрисковую ценную бумагу равна 0,1; в А – 0,36; в В – 0,54. Решение. Воспользуемся формулой А) Факторный риск портфеля Нефакторный риск портфеля: Стандартное отклонение портфеля: s Р = Б)
3. В рамках однофакторной модели ценная бумага А имеет чувствительность -0,50, а чувствительность ценной бумаги В равна 1,25. Если ковариация между этими ценными бумагами равна -312,50, то чему равно стандартное отклонение для фактора? Решение. Ковариация ценных бумаг i и j равняется:
4. В рамках однофакторной модели для двух ценных бумаг А и В имеют место соотношения: rA = 5% + 0,8 F + еА, rB =7%+ 1,2 F + еB; sF = 18%; seA = 25%; seB = 15%. Вычислите стандартное отклонение для каждой ценной бумаги. Решение.
5. Если средний нефакторный риск ( Решение.
6. В рамках трехфакторной модели рассмотрим портфель, состоящий из трех ценных бумаг со следующими характеристиками:
Каковы чувствительности портфеля к факторам 1, 2 и 3? Решение. К фактору 1 - к фактору 2 - к фактору 3 -
7. Портфель содержит два вида ценных бумаг. В рамках двухфакторной модели эти ценные бумаги имеют следующие характеристики:
Факторы являются некоррелированными. Фактор 1 имеет ожидаемое значение 15% и стандартное отклонение 20%. Фактор 2 имеет ожидаемое значение 4% и стандартное отклонение 5%. Вычислите ожидаемое значение и стандартное отклонение для портфеля. Решение. rA = 2+0,3×15+2×4=14,5, rB = 3+0,5×15+1,8×4=17,7, rP = 0,7×14,5+0,3×17,7=15,46.
то
8. Рассмотрим факторную модель, в которой двумя факторами являются отношение дохода к цене и отношение балансовой стоимости к рыночной цене. Для акций вида А первое отношение равно 10%, а второе 2. Для акций вида В эти показатели равны соответственно 15% и 0,90. Нулевые факторы для акций А и В равны 7 и 9% соответственно. Чему равны ожидаемые значения указанных факторов, если ожидаемые доходности для акций А и В равны 18 и 16,5% соответственно? Решение. rA = 7+10× F 1+2× F 2=18, rB = 9+15× F 1+0,9× F 2=16,5. Решаем эту систему уравнений и ответ: F 1=0,24, F 2=4,29.
9. В рамках двухфакторной модели рассмотрим два типа ценных бумаг со следующими характеристиками:
Стандартные отклонения факторов 1 и 2 равны 20 и 15% соответственно, а ковариация факторов равна 225. Каковы стандартные отклонения для ценных бумаг А и В? Чему равна их ковариация? Решение.
Задачи к теме «Факторные модели»
1. Рассмотрим в рамках однофакторной модели ценную бумагу со значением нулевого фактора 4% и чувствительностью к фактору, равной 0,50. Пусть значение фактора равно 10%. При этом доходность ценной бумаги составляет 11%. Какая часть доходности связана с нефакторными элементами? 2. В рамках однофакторной модели рассмотрим портфель из двух ценных бумаг со следующими характеристиками:
А) Если стандартное отклонение фактора равно 15%, то чему равен факторный риск Б) Ответьте на вопросы пункта А, предположив, что часть портфеля инвестирована в безрисковый актив и что доля инвестирования в безрисковую ценную бумагу равна 0,1; в А – 0,36; в В – 0,54. 3. В рамках однофакторной модели ценная бумага А имеет чувствительность -0,50, а чувствительность ценной бумаги В равна 1,25. Если ковариация между этими ценными бумагами равна -312,50, то чему равно стандартное отклонение для фактора? 4. В рамках однофакторной модели для двух ценных бумаг А и В имеют место соотношения: rA = 5% + 0,8 F + еА, rB =7%+ 1,2 F + еB; sF = 18%; seA = 25%; seB = 15%. Вычислите стандартное отклонение для каждой ценной бумаги. 5. Если средний нефакторный риск ( 6. В рамках трехфакторной модели рассмотрим портфель, состоящий из трех ценных бумаг со следующими характеристиками:
Каковы чувствительности портфеля к факторам 1, 2 и 3? 7. Портфель содержит два вида ценных бумаг. В рамках двухфакторной модели эти ценные бумаги имеют следующие характеристики:
Факторы являются некоррелированными. Фактор 1 имеет ожидаемое значение 15% и стандартное отклонение 20%. Фактор 2 имеет ожидаемое значение 4% и стандартное отклонение 5%. Вычислите ожидаемое значение и стандартное отклонение для портфеля. 8. Рассмотрим факторную модель, в которой двумя факторами являются отношение дохода к цене и отношение балансовой стоимости к рыночной цене. Для акций вида А первое отношение равно 10%, а второе 2. Для акций вида В эти показатели равны соответственно 15% и 0,90. Нулевые факторы для акций А и В равны 7 и 9% соответственно. Чему равны ожидаемые значения указанных факторов, если ожидаемые доходности для акций А и В равны 18 и 16,5% соответственно? 9. В рамках двухфакторной модели рассмотрим два типа ценных бумаг со следующими характеристиками:
Стандартные отклонения факторов 1 и 2 равны 20 и 15% соответственно, а ковариация факторов равна 225. Каковы стандартные отклонения для ценных бумаг А и В? Чему равна их ковариация?
|


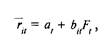 где rit - ожидаемая доходность акций типа i в период t при условии, что фактическое значение фактора равнялось Ft:
at — нулевой фактор в период t;
bit – ставка дивидендов акций типа i в период t;
Ft –фактическое значение фактора в период t.
Наклон, равный Ft, соответствует приросту ожидаемой доходности на каждый процент ставки дивиденда. Поэтому он представляет собой фактическое значение фактора ставки дивиденда (F) в рассматриваемом временном интервале.
где rit - ожидаемая доходность акций типа i в период t при условии, что фактическое значение фактора равнялось Ft:
at — нулевой фактор в период t;
bit – ставка дивидендов акций типа i в период t;
Ft –фактическое значение фактора в период t.
Наклон, равный Ft, соответствует приросту ожидаемой доходности на каждый процент ставки дивиденда. Поэтому он представляет собой фактическое значение фактора ставки дивиденда (F) в рассматриваемом временном интервале.

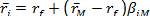
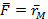 ):
):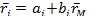
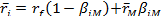
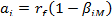 ,
,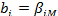 .
.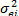 )
)
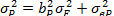
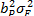 =(0,2×0,4+3,5×0,6)2152=4,7524×225=1069,29.
=(0,2×0,4+3,5×0,6)2152=4,7524×225=1069,29.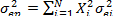 =(0,4)249+(0,6)2100=43,84.
=(0,4)249+(0,6)2100=43,84.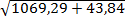 =33,36.
=33,36. =(0,36)249+(0,54)2100=35,51;. s Р= 30,03.
=(0,36)249+(0,54)2100=35,51;. s Р= 30,03. , откуда
, откуда 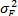 =312,5/(1,25×0,5)=500,
=312,5/(1,25×0,5)=500, 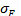 =22,36.
=22,36.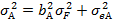 =(0,8×18)2+252=832,36,
=(0,8×18)2+252=832,36, 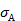 =28,85.
=28,85.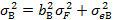 =(1,2×18)2+152=691,56,
=(1,2×18)2+152=691,56, 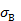 =26,3.
=26,3.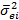 ) всех ценных бумаг в однофакторной модели равняется 225, то каков нефакторный риск портфеля, который включает 10, 100 или 1000 ценных бумаг с равным весом?
) всех ценных бумаг в однофакторной модели равняется 225, то каков нефакторный риск портфеля, который включает 10, 100 или 1000 ценных бумаг с равным весом?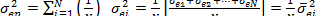 , откуда ответ: 22,5; 2,25; 0,225.
, откуда ответ: 22,5; 2,25; 0,225.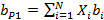 =0,6×0,2+0,2(0,5+1,5)=0,52;
=0,6×0,2+0,2(0,5+1,5)=0,52;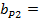 0,6×3,6+0,2(10+2,2)=4,6;
0,6×3,6+0,2(10+2,2)=4,6; 0,6×0,05+0,2(0,75+0,3)=0,24.
0,6×0,05+0,2(0,75+0,3)=0,24.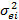 )
)
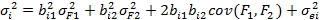 , так как
, так как 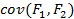 =0,
=0, =(0,3×20)2+(2×5)2+196=332,
=(0,3×20)2+(2×5)2+196=332, 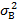 =(0,5×20)2+(1,8×5)2+100=281,
=(0,5×20)2+(1,8×5)2+100=281,
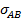 =0,3×0,5×400+2×1,8×25=60+90=150
=0,3×0,5×400+2×1,8×25=60+90=150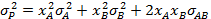 =250,97=15,82.
=250,97=15,82.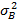 =(0,7×20)2+(1,2×15)2+2×0,7×1,2×225+16=196+324+378+16=914=30,232.
=(0,7×20)2+(1,2×15)2+2×0,7×1,2×225+16=196+324+378+16=914=30,232.