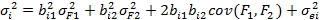Двухфакторные модели
Двухфакторная модель для периода t rit = ai + bi 1 F 1 t + bi 2 F 2 t + eit, где F 1 t и F 2 t – два фактора, оказывающих влияние на доходы по всем ценным бумагам, а bi 1 и bi 2 – чувствительности ценной бумаги i к этим двум факторам. Как и в случае однофакторной модели, eit – случайная ошибка, ai – ожидаемая доходность ценной бумаги i при условии, что каждый фактор имеет нулевое значение.
Смещение (нулевой фактор), равное на рисунке 5,8%, дает ожидаемую доходность для случая, когда и прирост ВВП, и инфляция равны нулю. Наконец, для конкретного года расстояние от фактической точки до плоскости равно специфической доходности в этом году (е.), т.е. той части доходности, которая не связана ни с приростом ВВП, ни с инфляцией.
В рамках двухфакторной модели для каждой ценной бумаги нужно оценить четыре параметра: a, b 1, b 2 и стандартное отклонение случайной ошибки, обозначаемое как sеi. Для каждого из_факторов нужно оценить два параметра — ожидаемое значение каждого фактора (
Ожидаемая доходность ценной бумаги i может быть вычислена по следующей формуле:
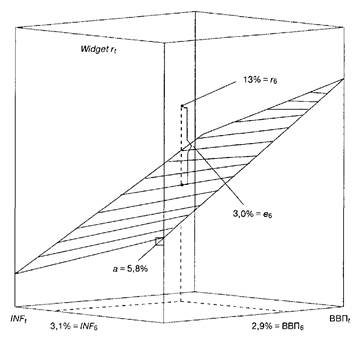
Дисперсия ценной бумаги i равна:
Ковариация ценных бумаг i и j определяется следующей формулой:
Все сказанное ранее относительно однофакторных моделей применимо и в случае диверсификации.
|

 1 и
1 и 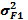 и
и  ). Наконец, нужно оценить ковариацию факторов – cov(F 1, F 2).
). Наконец, нужно оценить ковариацию факторов – cov(F 1, F 2).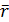 i = ai + bi 1
i = ai + bi 1  1 + bi 2
1 + bi 2