Расчет погрешностей прямых измерений
Систематические погрешности. Систематические ошибки закономерным образом изменяют значения измеряемой величины. Наиболее просто поддаются оценке погрешности, вносимые визмерения приборами, если они связаны с конструктивными особенностями самих приборов. Эти погрешности указываются в паспортах к приборам. Погрешности некоторых приборов можно оценить и не обращаясь к паспорту. Для многих электроизмерительных приборов непосредственно на шкале указаних класс точности. Класс точности прибора . Тогда абсолютная погрешность
Для электроизмерительных приборов введено 8 классов точности: 0,05; 0,1; 0,5; 1,0; 1,5; 2,0; 2,5; 4. Чем ближе измеряемая величина к номиналу, тем более точным будет результат измерения. Максимальная точность (т.е. наименьшая относительная ошибка), которую может обеспечить данный прибор, равна классу точности. Это обстоятельство необходимо учитывать при использовании многошкальных приборов. Шкалу надо выбирать с таким расчетом, чтобы измеряемая величина, оставаясь в пределах шкалы, была как можно ближе к номиналу. Если класс точности для прибора не указан, то необходимо руководствоваться следующими правилами: · Абсолютная погрешность приборов с нониусом равна точности нониуса. · Абсолютная погрешность приборов с фиксированным шагом стрелки равна цене деления[1]. · Абсолютная погрешность цифровых приборов равна единице минимального разряда. · Для всех остальных приборов абсолютная погрешность принимается равной половине цены деления. Случайные погрешности. Эти погрешности имеют статистический характер и описываются теорией вероятности. Установлено, что при очень большом количестве измерений вероятность получить тот или иной результат в каждом отдельном измерении можно определить при помощи нормального распределения Гаусса. При малом числе измерений математическое описание вероятности получения того или иного результата измерения называется распределением Стьюдента (более подробно об этом можно прочитать в пособии Скворцовой И.Л. «Ошибки измерений физических величин»). Как же оценить истинное значение измеряемой величины? Пусть при измерении некоторой величины 1). Вычисляется среднее арифметическое серии из N прямых измерений:
2). Вычисляется абсолютная случайная погрешность каждого измерения
3). Вычисляется средняя квадратичная абсолютная погрешность
4). Вычисляется абсолютная случайная погрешность
Коэффициент Стьюдента зависит от числа измерений N и коэффициента надежности Коэффициент надежности Доверительный интервал Таким образом, коэффициент Стъюдента – это число, на которое нужно умножить среднюю квадратичную погрешность, чтобы при данном числе измерений обеспечить заданную надежность результата. Чем большую надежность необходимо обеспечить для данного числа измерений, тем больше коэффициент Стъюдента. С другой стороны, чем больше число измерений, тем меньше коэффициент Стъюдента при данной надежности. В лабораторных работах нашего практикума будем считать надежность заданной и равной 0,9. Числовые значения коэффициентов Стъюдента при этой надежности для разного числа измерений приведены в таблице 1. Таблица 1
5).Вычисляется полная абсолютная погрешность. При любых измерениях существуют и случайные и систематические погрешности. Расчет общей (полной) абсолютной погрешности измерения дело непростое, так как эти погрешности разной природы. Для инженерных измерений имеет смысл суммировать систематическую и случайную абсолютные погрешности
Для простоты расчетов принято оценивать полную абсолютную погрешность как сумму абсолютной случайной и абсолютной систематической (приборной) погрешностей, если погрешности одного порядка величины, и пренебрегать одной из погрешностей, если она болеечем на порядок (в 10 раз) меньше другой. 6). Округляется погрешность и результат. Поскольку результат измерений представляется в виде интервала значений, величину которого определяет полная абсолютная погрешность, важное значение имеет правильное округление результата и погрешности. Округление начинают с абсолютной погрешности!!! Число значащих цифр, которое оставляют в значении погрешности, вообще говоря, зависит от коэффициента надежности и числа измерений. Однако даже для очень точных измерений (например, астрономических), в которых точное значение погрешности важно, не оставляют более двух значащих цифр. Бóльшее число цифр не имеет смысла, так как определение погрешности само имеет свою погрешность. В нашем практикуме сравнительно небольшой коэффициент надежности Разряд значащей цифры абсолоютной погрешности определяет разряд первой сомнительной цифры взначении результата. Следовательно, само значение результата нужно округлять (с поправкой) до той значащей цифры, разряд которой совпадает с разрядом значащей цифры погрешности. Сформулированное правило следует применять и в тех случаях, когда некоторые из цифр являются нулями. Пример. Если при измерении массы тела получен результат 7). Вычисляется относительная погрешность
При округлении относительной погрешности достаточно оставить две значащие цифры. результат серии измерений некоторой физической величины представляют в виде интервала значений с указанием вероятности попадания истинного значения в данный интервал,то есть результат необходимо записать в виде:
Здесь Рассмотрим несколько примеров: 1. Пусть при измерении длины отрезка мы получили следующий результат:
Результат измерений записываем так:
2. Пусть при расчете сопротивления проводника мы получили следующий результат:
Результат измерений записываем так:
3. Пусть при расчете массы груза мы получили следующий результат:
Результат измерений массы груза записываем так:
Из приведенных примеров видно, что округление абсолютной погрешности производится до первой значащей цифры в сторону увеличения (с избытком). Среднее значение измеряемой величины округляется с поправкой до той значащей цифры, разряд которой совпадает с разрядом значащей цифры погрешности. При округлении относительной погрешности оставляем две значащие цифры.
|

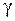 – это отношение абсолютной погрешности прибора
– это отношение абсолютной погрешности прибора 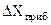 к максимальному значению измеряемой величины
к максимальному значению измеряемой величины 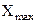 , которое можно определить с помощью данного прибора (это систематическая относительная погрешность данного прибора, выраженная в процентах от номинала шкалы
, которое можно определить с помощью данного прибора (это систематическая относительная погрешность данного прибора, выраженная в процентах от номинала шкалы 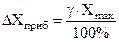 .
.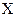 мы получили N результатов:
мы получили N результатов: 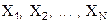 . Среднее арифметическое серии измерений ближе к истинному значению измеряемой величины, чем большинство отдельных измерений. Для получения результата измерения некоторой величины
. Среднее арифметическое серии измерений ближе к истинному значению измеряемой величины, чем большинство отдельных измерений. Для получения результата измерения некоторой величины 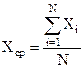 .
.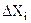 – это разность между средним арифметическим серии из N прямых измерений и данным измерением:
– это разность между средним арифметическим серии из N прямых измерений и данным измерением: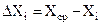 .
.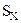 :
: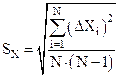 .
. . При небольшом числе измерений абсолютную случайную погрешность можно рассчитать через среднюю квадратичную погрешность
. При небольшом числе измерений абсолютную случайную погрешность можно рассчитать через среднюю квадратичную погрешность 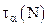 , называемый коэффициентом Стъюдента:
, называемый коэффициентом Стъюдента: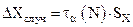 ,
,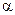 (в таблице 1 отражена зависимость коэффициента Стьюдента от числа измерений при фиксированном значении коэффициента надежности
(в таблице 1 отражена зависимость коэффициента Стьюдента от числа измерений при фиксированном значении коэффициента надежности 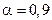 ).
).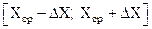 – это числовой интервал, в который с определенной вероятностью попадает истинное значение измеряемой величины.
– это числовой интервал, в который с определенной вероятностью попадает истинное значение измеряемой величины.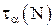
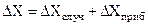 .
.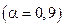 и малое число измерений. Поэтому при округлении (с избытком) полной абсолютной погрешности оставляют одну значащую цифру.
и малое число измерений. Поэтому при округлении (с избытком) полной абсолютной погрешности оставляют одну значащую цифру.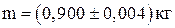 , то писать нули в конце числа 0,900 необходимо. Запись
, то писать нули в конце числа 0,900 необходимо. Запись 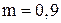 означала бы, что о следующих значащих цифрах ничего не известно, в то время как измерения показали, что они равны нулю.
означала бы, что о следующих значащих цифрах ничего не известно, в то время как измерения показали, что они равны нулю.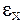 .
. .
. ;
; 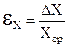 ;
; 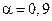 .
.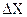 – полная, округленная до первой значащей цифры, абсолютная погрешность и
– полная, округленная до первой значащей цифры, абсолютная погрешность и 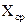 – округленное с учетом уже округленной погрешности среднее значение измеряемой величины. При записи результата измерений обязательно нужно указать единицу измерения величины.
– округленное с учетом уже округленной погрешности среднее значение измеряемой величины. При записи результата измерений обязательно нужно указать единицу измерения величины. см и
см и 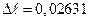 см. Как грамотно записать результат измерений длины отрезка? Сначала округляем с избытком абсолютную погрешность, оставляя одну значащую цифру
см. Как грамотно записать результат измерений длины отрезка? Сначала округляем с избытком абсолютную погрешность, оставляя одну значащую цифру 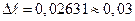 см. Значащая цифра погрешности в разряде сотых. Затем округляем с поправкой среднее значение с точностью до сотых, т.е. до той значащей цифры, разряд которой совпадает с разрядом значащей цифры погрешности
см. Значащая цифра погрешности в разряде сотых. Затем округляем с поправкой среднее значение с точностью до сотых, т.е. до той значащей цифры, разряд которой совпадает с разрядом значащей цифры погрешности 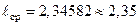 см. Вычисляем относительную погрешность
см. Вычисляем относительную погрешность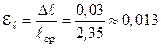 .
.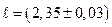 см;
см; 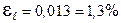 ;
;  и
и 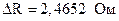 . Сначала округляем абсолютную погрешность, оставляя одну значащую цифру
. Сначала округляем абсолютную погрешность, оставляя одну значащую цифру 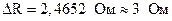 . Затем округляем среднее значение с точностью до целых
. Затем округляем среднее значение с точностью до целых 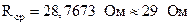 . Вычисляем относительную погрешность
. Вычисляем относительную погрешность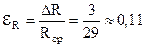 .
.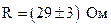 ;
;  ;
; 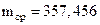 кг и
кг и 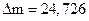 кг. Сначала округляем абсолютную погрешность, оставляя одну значащую цифру
кг. Сначала округляем абсолютную погрешность, оставляя одну значащую цифру 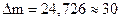 кг. Затем округляем среднее значение с точностью до десятков
кг. Затем округляем среднее значение с точностью до десятков  кг. Вычисляем относительную погрешность
кг. Вычисляем относительную погрешность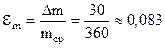 .
.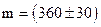 кг;
кг; 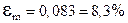 ;
; 


