Анализ устойчивости САУ. Критерии устойчивости
Анализ системы на устойчивость основан на решении однородного дифференциального уравнения, описывающего свободное движение:
Условием устойчивости является:
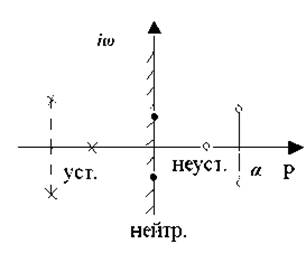
Если корни характеристического уравнения вещественные и разные, то выходная величина будет монотонно изменяться, а характер изменения каждой составляющей будет определяться знаком соответствующего корня. Если p i = 0, то i–я составляющая принимает постоянное во времени состояние. При p i > 0 соответствующая ему составляющая будет с течением времени увеличиваться до бесконечности. Следовательно, система будет устойчива только в том случае, если все корни характеристического уравнения меньше нуля.
Если корни характеристического уравнения сопряженные комплексные (p i = α i ± jω i), то составляющие переходного процесса будут иметь колебательный характер:
где А i и φ i – постоянные интегрирования. В этом случае система будет устойчива, если все вещественные части корней (α i) будут отрицательными, а амплитуда колебаний будет стремиться со временем к нулю. Корни характеристического уравнения легко определяются, если его степень не выше второй. Решение уравнений более высоких порядков связано с большими трудностями и выполняется с использованием численных методов. Поэтому были разработаны методы, позволяющие исследовать системы на устойчивость с помощью специальных критериев, не вычисляя при этом корней характеристического уравнения. Одним из таких критериев является алгебраический критерий Гурвица, который формулирует условие устойчивости в виде определителей. Для этого из коэффициентов характеристического уравнения составляют определитель.
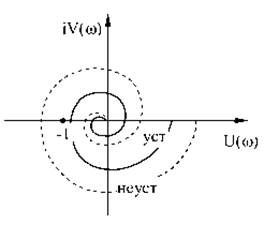
По алгебраическому критерию система n–порядка устойчива, если a1, а также все диагональные определители больше нуля. Критерий Гурвица позволяет только установить факт устойчивости, и по полученным значениям невозможно определить, насколько близко к границе устойчивости находится система. Критерий Найквиста (амплитудно-фазовый) был предложен для исследования устойчивости усилителей с обратной связью. Он позволяет судить об устойчивости замкнутой системы по поведению соответствующей ей разомкнутой системы, что упрощает расчеты.
Замкнутая система устойчива, если АФХ соответствующей ей разомкнутой системы W(jω) при изменении частоты от 0 до бесконечности не охватывает точки с координатами -1, i0. Достоинством критерия Найквиста является возможность оценить, как близко к границе устойчивости находится система.
|

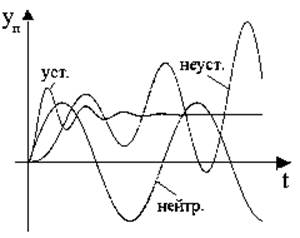 Практическая пригодность систем регулирования определяется их устойчивостью и приемлемым качеством регулирования. Под устойчивостью понимают способность системы возвращаться в исходное состояние при прекращении возмущающего воздействия. Система может быть устойчива при воздействиях любой величины (устойчивость в большом) или при некоторых ограниченных воздействиях (устойчивость в малом).
Практическая пригодность систем регулирования определяется их устойчивостью и приемлемым качеством регулирования. Под устойчивостью понимают способность системы возвращаться в исходное состояние при прекращении возмущающего воздействия. Система может быть устойчива при воздействиях любой величины (устойчивость в большом) или при некоторых ограниченных воздействиях (устойчивость в малом).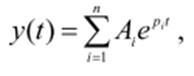
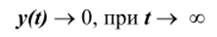
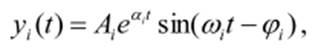
 По главной диагонали выписывают последовательно все коэффициенты характеристического уравнения, начиная с а1. Затем заполняют столбцы коэффициентами: вверх от главной диагонали – по возрастанию индексов до а n, вниз – по убыванию до а 0. Оставшиеся пустыми места заполняют нулями. Затем из матрицы выделяют диагональные определители, удаляя последовательно равное количество строк и столбцов.
По главной диагонали выписывают последовательно все коэффициенты характеристического уравнения, начиная с а1. Затем заполняют столбцы коэффициентами: вверх от главной диагонали – по возрастанию индексов до а n, вниз – по убыванию до а 0. Оставшиеся пустыми места заполняют нулями. Затем из матрицы выделяют диагональные определители, удаляя последовательно равное количество строк и столбцов.