Показатели надежности восстанавливаемых систем
Показатели безотказности. В соответствии с двумя способами задания потока отказов для восстанавливаемых систем можно применять различные показатели безотказности. При задании потока отказов как дискретного случайного процесса
Таким образом, параметр потока отказов – отношение числа отказов системы на некотором малом отрезке времени к значению этого отрезка. При значении потока отказов как последовательности случайных величин
Отметим, что в простейшем потоке средняя наработка на отказ Для статического определения средней наработки на отказ
Показатели ремонтопригодности. Ранее предполагалось, что продолжительностью восстановления можно пренебречь по сравнению с временем между отказами. На практике продолжительность восстановления почти всегда существенно меньше времени между отказами, однако нельзя не учитывать продолжительность восстановления для решения многих задач надежности (например, расчета потерь из-за отказов, количества необходимого ремонтного персонала и др.). Обозначим Тв случайную величину – продолжительность восстановление работоспособного состояние системы после отказа (далее сокращенно – время восстановления). Будем полагать, что распределение величины Тв не зависит ни от времени, ни от порядкового номера восстановления, ни от длительности предыдущего восстановления, ни от предшествующей наработки между отказами. Функцию распределения величины Тв G(t), плотность распределения g(t). Если к тому же наработки между отказами График функционирования системы с учетом времени восстановления дан на рис. 1.11. Для упрощения принято, что единственной причиной отключения системы являются ее отказы – отключения по всем иным причинам не рассматриваются. Показателем ремонтопригодности являются вероятность восстановления работоспособного состояния за заданное время t1 и среднее время восстановления соответственно
G(t1) =P{Tв < t1}; (1.40)
Статические определения этих показателей:
где l(t1) – число восстановлений, длительность которых меньше t1; m – общее число восстановлений; tвi – время восстановления после i-го отказа. Показатели долговечности. Календарную продолжительность от начала эксплуатации системы до перехода в предельное состояние называют сроком службы системы. Срок службы системы может быть случайной величиной, которую обозначим Tc .Тогда в качестве показателя долговечности можно принять средний срок службы
или гамма-процентный срок службы t P{Tc>t Таким образом t Для некоторых систем показателем долговечности является установленный срок службы, который должна достигнуть каждая система. Этот показатель можно интерпретировать как t В качестве случайной величины при рассмотрении долговечности может быть принят не только календарный срок службы системы, но и ее ресурс – наработка от начала эксплуатации до перехода в предельное состояние. Комплексные показатели надежности. Кроме приведенных выше показателей, каждый их которых характеризует одну из составляющих надежности, используются также комплексные показатели, отражающие совместно безотказность и ремонтопригодность. К ним относятся: коэффициент готовности kr , коэффициент оперативной готовности ko.r(t) и коэффициент технического пользования kт.н. Коэффициентом готовности kr называют вероятность того, что система окажется работоспособной в произвольно выбранный момент времени в установившемся в процессе эксплуатации. Можно показать (см., например, [1]), что в альтернирующем процессе восстановления коэффициента готовности kr= т.е. этот коэффициент численно равен средней доле времени, в течение которого система пребывает в работоспособном состоянии. Для статического определения, коэффициента готовности, как и в начале настоящего параграфа, поставим на испытания N одинаковых восстанавливаемых систем и обозначим Np(tx) число систем, находящихся в состоянии работоспособности в произвольный, достаточно удаленный от начала испытаний момент времени tx..Тогда статистическое определение коэффициента готовности
Коэффициентом оперативности готовности Примеры расчета: Стр. 68.
|

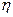 (t) – числа отказов в интервале (0,t) показателем безотказности является параметр потока отказов
(t) – числа отказов в интервале (0,t) показателем безотказности является параметр потока отказов 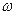 (t), определяемый соотношением (1.33). Для статического определения параметра потока отказов поставим на испытания N одинаковых восстанавливаемых систем в одинаковых условиях эксплуатации и при одинаковом техническом обслуживании. В момент t=0 все системы работоспособны и начинают работу. Будет пренебрегать продолжительностью восстановления. Обозначим ni(t) число отказов i-й системы (i =
(t), определяемый соотношением (1.33). Для статического определения параметра потока отказов поставим на испытания N одинаковых восстанавливаемых систем в одинаковых условиях эксплуатации и при одинаковом техническом обслуживании. В момент t=0 все системы работоспособны и начинают работу. Будет пренебрегать продолжительностью восстановления. Обозначим ni(t) число отказов i-й системы (i = 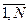 ) на интервале (0,t). Тогда
) на интервале (0,t). Тогда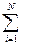 [ni (t +
[ni (t +  t) - ni(t)]/(N
t) - ni(t)]/(N 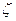 1,
1, 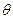 = М[
= М[ 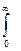 tf(t)dt (i = 1, 2…).
tf(t)dt (i = 1, 2…).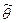 будем, как и выше, испытывать N одинаковых восстанавливаемых систем. Предположим, что каждая из них проработала в течении времени t. Тогда
будем, как и выше, испытывать N одинаковых восстанавливаемых систем. Предположим, что каждая из них проработала в течении времени t. Тогда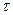 .
.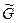 (t1)= l(t1)/m;
(t1)= l(t1)/m;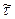 в =
в = 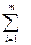 tвi /m, (1.41)
tвi /m, (1.41)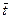 с= M[Tc]
с= M[Tc]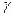 , который определяется соотношением
, который определяется соотношением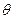 / (
/ (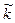 r = Np(tx) / N.
r = Np(tx) / N.



