Определить кинетическую энергию ядер кислорода, вылетающих под углом 30º к направлению бомбардирующих протонов в реакции 14N(p,n)14О, Q = -5,9 МэВ. Кинетическая энергия протонов 10 МэВ. Решение получить с помощью построенной в масштабе векторной диаграммы импульсов для ядерной реакции.
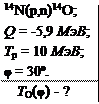 Решение
Решение
Так как кинетическая энергия вылетающих частиц в СЦИ не зависит от угла вылета, то делаем заключение, что следует определить кинетическую энергию Т О(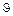 ) в ЛСК. Предварительно напомним, что в нерелятивистском случае, который здесь реализуется (почему?), кинетическая энергия ядер 14О выражается через их импульс обычным образом:
) в ЛСК. Предварительно напомним, что в нерелятивистском случае, который здесь реализуется (почему?), кинетическая энергия ядер 14О выражается через их импульс обычным образом:
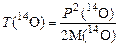 . .
| (3.11.1)
|
Для нахождения Р (14О) построим векторную диаграмму импульсов. Для этого определим величину вектора налетающей частицы:
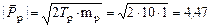 у.е.,
у.е.,
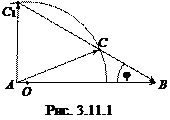 так как энергию и массу выражаем во внесистемных единицах. Выбираем в качестве масштаба 1 у.е. в 1 см и на рис. 3.11.1 строим направленный отрезок АВ длиной 4,47 см, отображающий вектор импульса налетающего протона. Затем делим этот отрезок точкой «О» на два отрезка АО и ОВ таким образом, чтобы АО: ОВ = mn: M(14O). По формуле (3.5), используя формулу (3.10.5), вычисляем величину импульса образовавшихся частиц в СЦИ.
так как энергию и массу выражаем во внесистемных единицах. Выбираем в качестве масштаба 1 у.е. в 1 см и на рис. 3.11.1 строим направленный отрезок АВ длиной 4,47 см, отображающий вектор импульса налетающего протона. Затем делим этот отрезок точкой «О» на два отрезка АО и ОВ таким образом, чтобы АО: ОВ = mn: M(14O). По формуле (3.5), используя формулу (3.10.5), вычисляем величину импульса образовавшихся частиц в СЦИ.
Радиусом R = 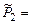 2,53 см проводим дугу с центром в точке «О». Из точки «В» под углом φ = 30º по отношению к отрезку АВ проводим луч до пересечения с дугой в точках «С» и «С 1». Направленные отрезки С 1 В и СВ отображают в ЛСК две возможные величины импульса вылетающих под углом φ = 30º ядер 14О. Соответственно отрезки АС 1 и АС отображают в ЛСК две возможные величины импульса образующихся нейтронов. Измерив длину отрезков С 1 В и СВ получаем, что Р 1(14О) = 5,0 у.е., а Р (14О) = 2,2 у.е. Этим величинам импульсов отвечают, согласно формуле (3.11.1), два значения кинетической энергии ядер 14О в ЛСК:
2,53 см проводим дугу с центром в точке «О». Из точки «В» под углом φ = 30º по отношению к отрезку АВ проводим луч до пересечения с дугой в точках «С» и «С 1». Направленные отрезки С 1 В и СВ отображают в ЛСК две возможные величины импульса вылетающих под углом φ = 30º ядер 14О. Соответственно отрезки АС 1 и АС отображают в ЛСК две возможные величины импульса образующихся нейтронов. Измерив длину отрезков С 1 В и СВ получаем, что Р 1(14О) = 5,0 у.е., а Р (14О) = 2,2 у.е. Этим величинам импульсов отвечают, согласно формуле (3.11.1), два значения кинетической энергии ядер 14О в ЛСК:
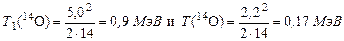 .
.
Полезно получить величины Р 1(14О) и Р 1(14О) аналитически. Для этого на рис. 3.11.1 соединим точки «О» и «С» и решим треугольник ОВС. Сторона ОС = 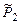 = 2,53 у.е., сторона ОВ =
= 2,53 у.е., сторона ОВ =  = (14/15) Ра = 4,17 у.е. Используя теорему косинусов, получим
= (14/15) Ра = 4,17 у.е. Используя теорему косинусов, получим
ОС 2 = СВ 2 + ОВ 2 – 2 СВ · ОВ · соs φ,
или квадратное уравнение для нахождения Р (14О):
2,532 = Р 2(14О) + 4,172 - 2 Р (14О)·  .
.
Это уравнение имеет два корня, которые дают две искомых величины векторов
Р 1(14О) = 3,61 + 1,43 = 5,04 у.е.
и
Р (14О) = 3,61 - 1,43 = 2,18 у.е.,
которые являются, разумеется, более точными, чем значения, полученные выше графическим способом.

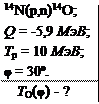 Решение
Решение ) в ЛСК. Предварительно напомним, что в нерелятивистском случае, который здесь реализуется (почему?), кинетическая энергия ядер 14О выражается через их импульс обычным образом:
) в ЛСК. Предварительно напомним, что в нерелятивистском случае, который здесь реализуется (почему?), кинетическая энергия ядер 14О выражается через их импульс обычным образом: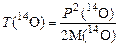 .
.
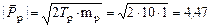 у.е.,
у.е.,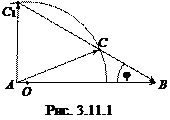 так как энергию и массу выражаем во внесистемных единицах. Выбираем в качестве масштаба 1 у.е. в 1 см и на рис. 3.11.1 строим направленный отрезок АВ длиной 4,47 см, отображающий вектор импульса налетающего протона. Затем делим этот отрезок точкой «О» на два отрезка АО и ОВ таким образом, чтобы АО: ОВ = mn: M(14O). По формуле (3.5), используя формулу (3.10.5), вычисляем величину импульса образовавшихся частиц в СЦИ.
так как энергию и массу выражаем во внесистемных единицах. Выбираем в качестве масштаба 1 у.е. в 1 см и на рис. 3.11.1 строим направленный отрезок АВ длиной 4,47 см, отображающий вектор импульса налетающего протона. Затем делим этот отрезок точкой «О» на два отрезка АО и ОВ таким образом, чтобы АО: ОВ = mn: M(14O). По формуле (3.5), используя формулу (3.10.5), вычисляем величину импульса образовавшихся частиц в СЦИ.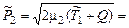
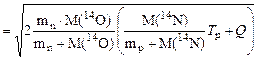 =
=
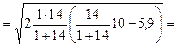 2,53 у.е.
2,53 у.е.
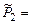 2,53 см проводим дугу с центром в точке «О». Из точки «В» под углом φ = 30º по отношению к отрезку АВ проводим луч до пересечения с дугой в точках «С» и «С 1». Направленные отрезки С 1 В и СВ отображают в ЛСК две возможные величины импульса вылетающих под углом φ = 30º ядер 14О. Соответственно отрезки АС 1 и АС отображают в ЛСК две возможные величины импульса образующихся нейтронов. Измерив длину отрезков С 1 В и СВ получаем, что Р 1(14О) = 5,0 у.е., а Р (14О) = 2,2 у.е. Этим величинам импульсов отвечают, согласно формуле (3.11.1), два значения кинетической энергии ядер 14О в ЛСК:
2,53 см проводим дугу с центром в точке «О». Из точки «В» под углом φ = 30º по отношению к отрезку АВ проводим луч до пересечения с дугой в точках «С» и «С 1». Направленные отрезки С 1 В и СВ отображают в ЛСК две возможные величины импульса вылетающих под углом φ = 30º ядер 14О. Соответственно отрезки АС 1 и АС отображают в ЛСК две возможные величины импульса образующихся нейтронов. Измерив длину отрезков С 1 В и СВ получаем, что Р 1(14О) = 5,0 у.е., а Р (14О) = 2,2 у.е. Этим величинам импульсов отвечают, согласно формуле (3.11.1), два значения кинетической энергии ядер 14О в ЛСК: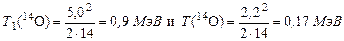 .
.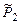 = 2,53 у.е., сторона ОВ =
= 2,53 у.е., сторона ОВ =  = (14/15) Ра = 4,17 у.е. Используя теорему косинусов, получим
= (14/15) Ра = 4,17 у.е. Используя теорему косинусов, получим .
.


