Задача 3.6
Получить формулу (3.6). Решение Из формулы (3.3) получаем выражение для вычисления энергии реакции:
где Т 1= Tа + TА и М 1 = mа + МА, Т 2 = mb + МB и М 2 = mb + МB, – суммарные кинетические энергии и суммарные энергии покоя частиц до и после реакции, которое имеет место в любой инерциальной системе отсчета. Определим порог реакции как минимальное значение кинетической энергии (Та)пор налетающей частицы а (частица А покоится!) в ЛСК, при которой кинетические энергии образовавшихся частиц b и В равна нулю в СЦИ. Для решения задачи удобно воспользоваться релятивистским инвариантом Е 2 – Р 2 с 2 = inv, который сохраняется для любой изолированной системы в любой инерциальной системе отсчета. Здесь Е = М + Т и Р – полная энергия и импульс произвольной системы тел, взаимодействующих только между собой. Инвариант системы до реакции при пороговой энергии (Та)пор в ЛСК:
но
откуда
Подставляя полученное выражение в (3.2) и выполняя необходимые преобразования, получим:
Инвариант для частиц с энергией покоя М 2, образовавшихся в результате эндоэнергетической реакции, в СЦИ будет равет:
так как их кинетическая энергия в СЦИ при пороговой кинетической энергии (Та)пор равна нулю. Приравнивая инварианты (3.6.3) и (3.6.4), получим
так как согласно (3.6.1) (M 2 – M 1) = | Q |. Второе слагаемое в (3.6.5) при | Q | < 100 МэВ ничтожно мало по сравнению с первым, и поэтому
Однако оно становиться значимым при расчете пороговой энергии ядерных реакций, приводящих к рождению барионов и гиперонов. Решим эту же задачу, используя законы классической (не релятивистской) механики. Законы сохранения энергии и импульса при пороговом значении кинетической энергии налетающей в ЛСК частицы а:
Т 2 и Р 2 определяют движение центра инерции образовавшихся частиц, так как их взаимная кинетичечкая энергия равна нулю при Та = (Та)пор. Используем классическую связь между импульсом и кинетической энергией
так как полагаем, что зависимостью массы системы от скорости можно пренебречь и поэтому скорости движения частиц много меньше скорости света. Действительно, даже если кинетическая энергия (Та)пор налетающей частицы а полностью переходит во внутреннюю энергию и изменяет массу системы, то Δ М = М 2 – М 1 ≤ (Та)пор, так как (Та)пор << М 1, при энергиях налетающих частиц менее 100 МэВ. Поэтому, при кинематических расчетах в нерялитивистском случае можно считать, что
Тогда, из (3.6.1), (3.6.8) и (3.6.9) получаем
Или, учитывая (3.6.10),
Полученная формула (3.6.12) является приближенной и ее отличие от точной формулы (3.6.5) вызвано пренебрежением релятивистским изменением массы.
|

 ,
,
 = [ mа + (Та)пор]2,
= [ mа + (Та)пор]2, + 2 mа ·(Та)пор.
+ 2 mа ·(Та)пор.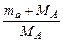 | Q | +
| Q | +  ,
,
 ,
,
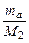 (Та)пор =
(Та)пор =  ,
,
 .
.



