Законы сохранения в ядерных реакциях
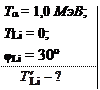 α-Частица с кинетической энергией Т α = 1,0 МэВ упруго рассеялась на покоящемся ядре 6Li. Определить кинетическую энергию ядра отдачи, отлетевшего под углом φ = 30º к первоначальному направлению движения α-частицы.
α-Частица с кинетической энергией Т α = 1,0 МэВ упруго рассеялась на покоящемся ядре 6Li. Определить кинетическую энергию ядра отдачи, отлетевшего под углом φ = 30º к первоначальному направлению движения α-частицы.
Решение
Запишем законы сохранения энергии и импульса:
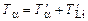 ; ;
| (3.1.1)
|
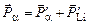 . .
| (3.1.2)
|
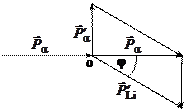 Изобразим графически закон сохранения импульса для процесса упругого рассеяния α-частицы на покоившимся ядре 6Li, которое произошло в точке «о». Верхние правые индексы «′» обозначают величины после рассеяния.
Изобразим графически закон сохранения импульса для процесса упругого рассеяния α-частицы на покоившимся ядре 6Li, которое произошло в точке «о». Верхние правые индексы «′» обозначают величины после рассеяния.
По теореме косинусов
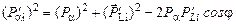 . .
| (3.1.3)
|
Так как энергия покоя частиц М с 2 >> Т α, то можно использовать классическую связь между импульсом и кинетической энергий. Тогда (3.1.3) приобретает вид:
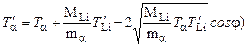 . .
| (3.1.4)
|
Выразим 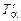 из (3.1.1), подставим в уравнение (3.1.4) и, освободившись от иррациональности, получим
из (3.1.1), подставим в уравнение (3.1.4) и, освободившись от иррациональности, получим
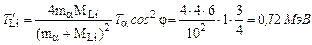 . .
| (3.1.5)
|
 Эта же задача может быть решена с помощью векторной диаграммы импульсов для упругого рассеяния, построение которой приведено на рис. 3.1. Построение векторной диаграммы импульсов для поставленной задачи изображено на рисунке слева. Энергия ядра 6Li после соударения выражается через его импульс следующим образом
Эта же задача может быть решена с помощью векторной диаграммы импульсов для упругого рассеяния, построение которой приведено на рис. 3.1. Построение векторной диаграммы импульсов для поставленной задачи изображено на рисунке слева. Энергия ядра 6Li после соударения выражается через его импульс следующим образом
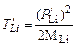 . .
| (3.1.6)
|
Но длина отрезка CB соответствует величине импульса 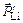 . Для нахождения отрезка CB используем равнобедренный треугольник COВ:
. Для нахождения отрезка CB используем равнобедренный треугольник COВ:
СВ = 2ОВ·cosφ.
Тогда
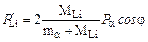 .
.
Подставляя последнее выражение в (3.1.6), получим окончательно
Полученное выражение для энергии 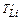 полностью совпадает с выражением (3.1.5), но получено гораздо проще, что и определяет применение векторной диаграммы импульсов.
полностью совпадает с выражением (3.1.5), но получено гораздо проще, что и определяет применение векторной диаграммы импульсов.

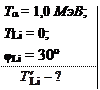 α-Частица с кинетической энергией Т α = 1,0 МэВ упруго рассеялась на покоящемся ядре 6Li. Определить кинетическую энергию ядра отдачи, отлетевшего под углом φ = 30º к первоначальному направлению движения α-частицы.
α-Частица с кинетической энергией Т α = 1,0 МэВ упруго рассеялась на покоящемся ядре 6Li. Определить кинетическую энергию ядра отдачи, отлетевшего под углом φ = 30º к первоначальному направлению движения α-частицы.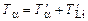 ;
;
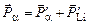 .
.
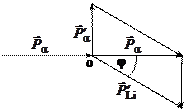 Изобразим графически закон сохранения импульса для процесса упругого рассеяния α-частицы на покоившимся ядре 6Li, которое произошло в точке «о». Верхние правые индексы «′» обозначают величины после рассеяния.
Изобразим графически закон сохранения импульса для процесса упругого рассеяния α-частицы на покоившимся ядре 6Li, которое произошло в точке «о». Верхние правые индексы «′» обозначают величины после рассеяния.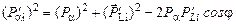 .
.
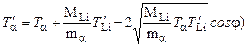 .
.
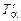 из (3.1.1), подставим в уравнение (3.1.4) и, освободившись от иррациональности, получим
из (3.1.1), подставим в уравнение (3.1.4) и, освободившись от иррациональности, получим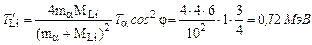 .
.
 Эта же задача может быть решена с помощью векторной диаграммы импульсов для упругого рассеяния, построение которой приведено на рис. 3.1. Построение векторной диаграммы импульсов для поставленной задачи изображено на рисунке слева. Энергия ядра 6Li после соударения выражается через его импульс следующим образом
Эта же задача может быть решена с помощью векторной диаграммы импульсов для упругого рассеяния, построение которой приведено на рис. 3.1. Построение векторной диаграммы импульсов для поставленной задачи изображено на рисунке слева. Энергия ядра 6Li после соударения выражается через его импульс следующим образом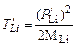 .
.
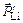 . Для нахождения отрезка CB используем равнобедренный треугольник COВ:
. Для нахождения отрезка CB используем равнобедренный треугольник COВ: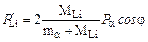 .
.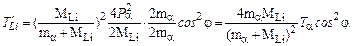
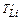 полностью совпадает с выражением (3.1.5), но получено гораздо проще, что и определяет применение векторной диаграммы импульсов.
полностью совпадает с выражением (3.1.5), но получено гораздо проще, что и определяет применение векторной диаграммы импульсов.


