Построить векторные диаграммы импульсов для упругого рассеяния нерелятивистской α-частицы на покоящемся ядре:
а) 6Li, 4Не, 2Н, если угол рассеяния в α-частицы в СЦИ равен 60º. В каком случае связь между кинетической энергией рассеянной α-частицы и углом ее рассеяния неоднозначна? Найти для этих трех случаев значения максимально возможного угла рассеяния α-частицы.
Решение
Для анализа упругого рассеяния α-частицы построим векторные диаграммы импульсов для всех трех случаев.
а) рассеяние α-частицы на ядре 6Li.
 Отрезок АВ, изображающий импульс налетающей α-частицы, делим на 5 равных частей, т.к. mα: M(6Li) = 2: 3. От точки А отсчитываем две части и ставим точку О. Из точки О радиусом ОВ проводим дугу ВD. Под углом
Отрезок АВ, изображающий импульс налетающей α-частицы, делим на 5 равных частей, т.к. mα: M(6Li) = 2: 3. От точки А отсчитываем две части и ставим точку О. Из точки О радиусом ОВ проводим дугу ВD. Под углом 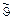 = 60º из точки О проводим луч до пересечения с дугой ВD. Точку пересечения обозначаем буквой С и соединяем ее с точками А и В. Полученный отрезок АС и угол
= 60º из точки О проводим луч до пересечения с дугой ВD. Точку пересечения обозначаем буквой С и соединяем ее с точками А и В. Полученный отрезок АС и угол 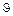 изображают величину импульса α-частицы и направление ее движения после рассеяния в ЛСК, а отрезок СВ – и угол φ величину импульс ядра и направление движения ядра 6Li после соударения также в ЛСК. Для различных параметров удара точка С может располагаться на дуге ВD в любом месте от точки B и до точки D. При этом величина импульса α-частицы после рассеяния (длина отрезка АС) однозначно связана с углом
изображают величину импульса α-частицы и направление ее движения после рассеяния в ЛСК, а отрезок СВ – и угол φ величину импульс ядра и направление движения ядра 6Li после соударения также в ЛСК. Для различных параметров удара точка С может располагаться на дуге ВD в любом месте от точки B и до точки D. При этом величина импульса α-частицы после рассеяния (длина отрезка АС) однозначно связана с углом 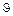 или углом
или углом 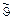 . Следовательно и кинетическая энергия T = P 2/2 m в этом случае является однозначной функцией угла рассеяния а обеих системах координат. Максимальные углы рассеяния
. Следовательно и кинетическая энергия T = P 2/2 m в этом случае является однозначной функцией угла рассеяния а обеих системах координат. Максимальные углы рассеяния 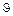 и
и 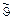 в этом случае определяются положением точки С при ее совпадении с точкой D и равны π.
в этом случае определяются положением точки С при ее совпадении с точкой D и равны π.
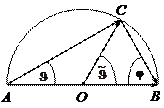 б) Рассеяние α-частицы на ядре 4Не.
б) Рассеяние α-частицы на ядре 4Не.
Так как массы сталкивающихся частиц равны, то отрезок АВ делим на две равные части и проводим дугу ВD с центром в точке О. Далее построения не отличаются от построений в предыдущем пункте задачи. В этом случае связь кинетической энергии рассеянной α-частицы с углами рассеяния оказывается также однозначной в обеих системах координат. Предельное значение угла 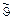 также стремиться к π. Однако, как нетрудно заметить, предельное значение угла
также стремиться к π. Однако, как нетрудно заметить, предельное значение угла 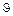 стремиться к π/2. Из этого следует важный вывод о том, что угол рассеяния двух тел с одинаковой массой не может превышать π/2.
стремиться к π/2. Из этого следует важный вывод о том, что угол рассеяния двух тел с одинаковой массой не может превышать π/2.
в) рассеяние α-частицы на ядре 2Н.
 Отрезок АВ, изображающий импульс налетающей α-частицы, делим на 3 равных части, т.к. mα: M(2Н) = 2: 1. От точки А отсчитываем две части и ставим точку О. Далее построения не отличаются от построений в предыдущих пунктах а) и б). Из диаграммы следует, что одному значению угла
Отрезок АВ, изображающий импульс налетающей α-частицы, делим на 3 равных части, т.к. mα: M(2Н) = 2: 1. От точки А отсчитываем две части и ставим точку О. Далее построения не отличаются от построений в предыдущих пунктах а) и б). Из диаграммы следует, что одному значению угла 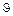 рассеяния в ЛСК соответствуют две возможные величины импульса рассеянной α-частицы (отрезки AD и АС), а, следовательно, и два возможных значения кинетической энергии рассеянной α-частицы. Максимальное значение угла
рассеяния в ЛСК соответствуют две возможные величины импульса рассеянной α-частицы (отрезки AD и АС), а, следовательно, и два возможных значения кинетической энергии рассеянной α-частицы. Максимальное значение угла 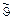 рассеяния α-частицы в СЦИ будет равно π. В ЛСК максимальное значение угла
рассеяния α-частицы в СЦИ будет равно π. В ЛСК максимальное значение угла 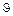 определяется положением касательной
определяется положением касательной 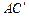 . Из прямоугольного треугольника
. Из прямоугольного треугольника  сразу следует, что
сразу следует, что

и, следовательно,
 .
.

 Отрезок АВ, изображающий импульс налетающей α-частицы, делим на 5 равных частей, т.к. mα: M(6Li) = 2: 3. От точки А отсчитываем две части и ставим точку О. Из точки О радиусом ОВ проводим дугу ВD. Под углом
Отрезок АВ, изображающий импульс налетающей α-частицы, делим на 5 равных частей, т.к. mα: M(6Li) = 2: 3. От точки А отсчитываем две части и ставим точку О. Из точки О радиусом ОВ проводим дугу ВD. Под углом 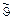 = 60º из точки О проводим луч до пересечения с дугой ВD. Точку пересечения обозначаем буквой С и соединяем ее с точками А и В. Полученный отрезок АС и угол
= 60º из точки О проводим луч до пересечения с дугой ВD. Точку пересечения обозначаем буквой С и соединяем ее с точками А и В. Полученный отрезок АС и угол 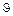 изображают величину импульса α-частицы и направление ее движения после рассеяния в ЛСК, а отрезок СВ – и угол φ величину импульс ядра и направление движения ядра 6Li после соударения также в ЛСК. Для различных параметров удара точка С может располагаться на дуге ВD в любом месте от точки B и до точки D. При этом величина импульса α-частицы после рассеяния (длина отрезка АС) однозначно связана с углом
изображают величину импульса α-частицы и направление ее движения после рассеяния в ЛСК, а отрезок СВ – и угол φ величину импульс ядра и направление движения ядра 6Li после соударения также в ЛСК. Для различных параметров удара точка С может располагаться на дуге ВD в любом месте от точки B и до точки D. При этом величина импульса α-частицы после рассеяния (длина отрезка АС) однозначно связана с углом 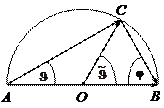 б) Рассеяние α-частицы на ядре 4Не.
б) Рассеяние α-частицы на ядре 4Не. Отрезок АВ, изображающий импульс налетающей α-частицы, делим на 3 равных части, т.к. mα: M(2Н) = 2: 1. От точки А отсчитываем две части и ставим точку О. Далее построения не отличаются от построений в предыдущих пунктах а) и б). Из диаграммы следует, что одному значению угла
Отрезок АВ, изображающий импульс налетающей α-частицы, делим на 3 равных части, т.к. mα: M(2Н) = 2: 1. От точки А отсчитываем две части и ставим точку О. Далее построения не отличаются от построений в предыдущих пунктах а) и б). Из диаграммы следует, что одному значению угла 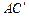 . Из прямоугольного треугольника
. Из прямоугольного треугольника  сразу следует, что
сразу следует, что
 .
.


