Законы логики.Равносильности формул логики высказываний часто называют законами логики. Перечислим наиболее важные из них: 1). 2). 3). 4). 5). a Ù a º a; a Ù a º a – законы идемпотентности. 6). a Ù b º b Ù a; a Ú b º b Ú a – законы коммутативности (переместительности). 7). (a Ù b) Ù c º a Ù (b Ù c); (a Ú b) Ú c º a Ú (b Ú c) – законы ассоциативности (сочетательности). 8). a Ù (b Ú c) º (a Ù b) Ú (a Ù c); a Ú (b Ù c) º (a Ú b) Ù (a Ú c) – законы дистрибутивности (распределительности). 9).
Закон тождества утверждает, что мысль, заключенная в некотором высказывании, остается (считается) неизменной на протяжении всего рассуждения, в котором это высказывание применяется. Закон противоречия говорит о том, что никакое предложение не может быть истинным одновременно со своим отрицанием. Утверждать, что какое-либо высказывание истинно вместе с его отрицанием, значит утверждать заведомую ложь. Если мы знаем, что в предложениях «Эта функция – периодическая» и «Эта функция – непериодическая» речь идет об одной и той же функции и первое предложение истинно, то, согласно закону противоречия, второе предложение ложно. Закон исключенного третьего говорит о том, что для каждого высказывания имеются лишь две возможности: это высказывание истинно или ложно; третьего не дано. Согласно закону двойного отрицания, отрицать отрицание какого-нибудь высказывания — то же, что утверждать это высказывание. Например, высказывание «Неверно, что 2*2 <>4» означает то же, что и «2*2=4». Законы коммутативности и ассоциативности конъюнкции и дизъюнкции аналогичны одноименным законам умножения и сложения чисел. Иногда дизъюнкцию так и называют логическим сложением, а конъюнкцию — логическим умножением. В отличие от сложения и умножения чисел логические сложение и умножение равноправны по отношению к дистрибутивности: не только конъюнкция дистрибутивна относительно дизъюнкции, но и дизъюнкция дистрибутивна относительно конъюнкции. В силу законов идемпотентности в алгебре логики нет «показателей степеней» и «коэффициентов»: конъюнкция одинаковых «сомножителей» равносильна одному из них; дизъюнкция одинаковых «слагаемых» равносильна одному из них. Смысл законов де Моргана можно выразить в кратких словесных формулировках: отрицание конъюнкции равносильно дизъюнкции отрицаний; отрицание дизъюнкции равносильно конъюнкции отрицаний. Упражнение. Докажем равносильность двух логических функций. Построим таблицы истинности логических выражений А Ú (В Ù С)
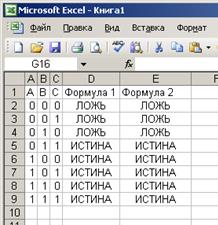
Эти формулы записываем в ячейки таблицы D2 и Е2 учитывая адреса ячеек в которых расположены логические переменные.
Колонки с формулами имеют одинаковые значения, следовательно, обе формулы равносильны.
|
– закон тождества.
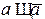º ложь – закон противоречия.
º истина – закон исключения третьего.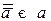
– закон двойного отрицания.
– законы де Моргана.
