Матрица линейного оператора.
Рассмотрим линейный оператор A:C®C (линейное преобразование пространства C). Пусть векторы
В результате получаем матрицу:
i- ый столбец которой есть вектор-столбец из координат вектора Пусть теперь
Таким образом, действие линейного оператора на вектор сводится к преобразованию его координат с помощью матрицы линейного оператора. Задание матрицы линейного оператора является наиболее удобным способом определения оператора действующего в конечномерном пространстве. Пусть С- матрица перехода от базиса
Матрицы Действиям над линейными операторами соответствуют точно такие же действия над их матрицами. Если А и В линейные операторы, действующие в Х и 1. Оператору А+В соответствует матрица 2. Оператору 3. Оператору АВ соответствует матрица 4.Если оператор В=А-1 , то матрица Пример 1. Вычислим матрицу тождественного оператора Е. По определению
Пример 2. Покажем, что поворот плоскости на угол a вокруг начала координат является линейным преобразованием, и найдем матрицу этого преобразования в любом ортонормированном базисе. Предполагается, что положительное направление отсчета углов совпадает с направлением кратчайшего поворота, переводящего базисный вектор
Образ вектора
Рассмотрим теперь сумму двух векторов
Тогда образ суммы
т. е. выполняется свойство аддитивности линейного оператора. Аналогично можно проверить выполнение свойства однородности
Пример 3. Линейный оператор А в базисе
имеет матрицу
Необходимо найти матрицу этого оператора в базисе Векторы двух базисов «старого»
Тогда матрица оператора А в «новом» базисе
Задачи 1. Пусть А и В- линейные операторы, действующие из Х в U. Показать, что оператор С=А+В является линейным.
2. Показать, что сложение операторов обладает следующими свойствами: А+В=В+А, (А+В)+С=А+(В+С). 3. Пусть А и В- линейные операторы. Показать, что оператор С=АВ является линейным. 4. Выяснить, какие из следующих операторов А, определенных путем задания координат вектора а) 5. Доказать, что существует единственное линейное преобразование трехмерного пространства, переводящее векторы
6. Линейное преобразование j в базисе Найти его матрицу в базисе 7. Пусть оператор А в базисе 8. Доказать, что любое линейное преобразование А одномерного пространства сводится к умножению всех векторов на одно и то же число, т.е. 9. Как изменится матрица линейного оператора, если в базисе
|

 образуют базис пространства C. Подействуем оператором А на базисные векторы. В результате получим векторы
образуют базис пространства C. Подействуем оператором А на базисные векторы. В результате получим векторы  . Так как вектор
. Так как вектор  , то его можно разложить по базису:
, то его можно разложить по базису: .
.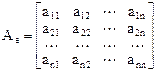 ,
, в базисе
в базисе  называется матрицей линейного оператора
называется матрицей линейного оператора  в заданном базисе
в заданном базисе 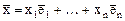 - произвольный вектор из C, а
- произвольный вектор из C, а 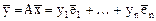 - его образ при линейном преобразовании А. Тогда координаты векторов
- его образ при линейном преобразовании А. Тогда координаты векторов 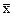 и
и  связаны соотношением:
связаны соотношением: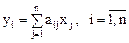 .
.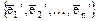 ,а
,а 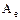 и
и 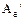 - матрицы оператора в первом и втором базисе соответственно. Тогда имеют место соотношения:
- матрицы оператора в первом и втором базисе соответственно. Тогда имеют место соотношения: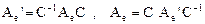 .
.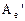 , связанные между собой данными соотношениями, называются подобными матрицами.
, связанные между собой данными соотношениями, называются подобными матрицами. - матрицы этих операторов в одном и том же базисе, то:
- матрицы этих операторов в одном и том же базисе, то: .
.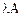 соответствует матрица
соответствует матрица  .
.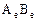 .
. .
.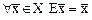 . Пусть
. Пусть 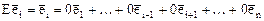 . Поэтому тождественному оператору соответствует единичная матрица:
. Поэтому тождественному оператору соответствует единичная матрица: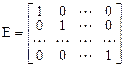 .
.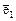 во второй вектор базиса
во второй вектор базиса  . Покажем, во-первых, что данный оператор является линейным. Пусть
. Покажем, во-первых, что данный оператор является линейным. Пусть 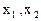 , модуль через r, угол с базисным вектором
, модуль через r, угол с базисным вектором  .
.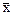 вектор
вектор  будет равен
будет равен

 .
.
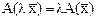 . Найдем теперь матрицу оператора в базисе
. Найдем теперь матрицу оператора в базисе 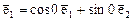 и
и 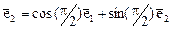 . Тогда образы базисных векторов равны
. Тогда образы базисных векторов равны  и
и  . Откуда матрица оператора имеет вид
. Откуда матрица оператора имеет вид .
. ,
, 
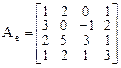 .
.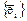 и «нового»
и «нового»  связаны соотношениями
связаны соотношениями  . Поэтому матрица перехода С от базиса
. Поэтому матрица перехода С от базиса  .
.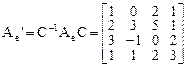 .
.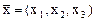 , являются линейными, и найти их матрицы в том же базисе, в котором заданы координаты вектора
, являются линейными, и найти их матрицы в том же базисе, в котором заданы координаты вектора 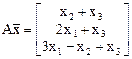 b)
b)  с)
с) 
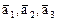 соответственно в
соответственно в 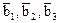 и найти матрицу этого преобразования в том же базисе, в котором заданы координаты всех векторов:
и найти матрицу этого преобразования в том же базисе, в котором заданы координаты всех векторов:

 ,
, 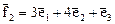 ,
, 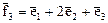 .
. имеет матрицу
имеет матрицу  , оператор В в базисе
, оператор В в базисе 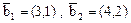 имеет матрицу
имеет матрицу 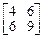 . Найти матрицу оператора А+В в базисе
. Найти матрицу оператора А+В в базисе 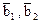 .
.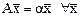 .
.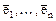 поменять местами векторы
поменять местами векторы 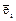 и
и 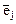 ?
?


