ЛИНЕЙНЫЕ ОПЕРАТОРЫ. МАТРИЦА ЛИНЕЙНОГО ОПЕРАТОРА.
Определение оператора. Действия с операторами.
Определение 1. Пусть C и U - линейные пространства, заданные над одним и тем же полем R. Отображение A: C ® U, ставящее в соответствие каждому элементу 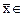 C некоторый элемент
C некоторый элемент 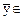 U, называется оператором, действующим из C в U. При этом используются обозначения
U, называется оператором, действующим из C в U. При этом используются обозначения 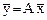 или
или 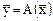 .
.
Определение 2. Оператор A, действующий из C в U, называется линейным, если  и
и 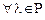 выполняются соотношения
выполняются соотношения
1. 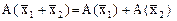 -свойство аддитивности оператора.
-свойство аддитивности оператора.
2.  - свойство однородности оператора.
- свойство однородности оператора.
Если пространство U совпадает с C, то линейный оператор A:C®C называют линейным преобразованием пространства C.
Пример 1. Поставим в соответствие каждому вектору 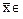 C этот же вектор
C этот же вектор 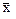 .Получим линейный оператор E: C®C, который называется тождественным или единичным оператором.
.Получим линейный оператор E: C®C, который называется тождественным или единичным оператором.
Пример 2. Пусть  . Пусть
. Пусть 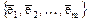 - ортонормированный базис в
- ортонормированный базис в 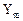 , а
, а 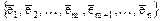 - его расширение до базиса в
- его расширение до базиса в  . Поставим в соответствие каждому вектору
. Поставим в соответствие каждому вектору 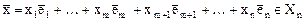 вектор
вектор  , определив его следующим образом
, определив его следующим образом 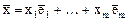 . Полученное отображение – линейный оператор, который называется оператором проектирования на подпространство.
. Полученное отображение – линейный оператор, который называется оператором проектирования на подпространство.
Определение 3. Два оператора  и
и 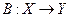 называются равными, если
называются равными, если  .
.
Определение 4. Оператор 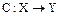 называется суммой операторов
называется суммой операторов  и
и 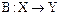 (
(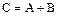 ), если
), если 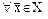
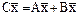 .
.
Определение 5. Оператор 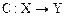 называется произведением оператора
называется произведением оператора  на число
на число 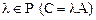 , если
, если 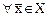
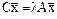 .
.
Определение 6. Оператор  называется произведением операторов
называется произведением операторов  и
и  (С=ВА), если
(С=ВА), если 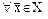
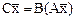 .
.

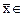 C некоторый элемент
C некоторый элемент 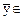 U, называется оператором, действующим из C в U. При этом используются обозначения
U, называется оператором, действующим из C в U. При этом используются обозначения 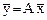 или
или 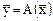 .
. и
и 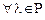 выполняются соотношения
выполняются соотношения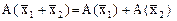 -свойство аддитивности оператора.
-свойство аддитивности оператора. - свойство однородности оператора.
- свойство однородности оператора.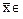 C этот же вектор
C этот же вектор 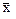 .Получим линейный оператор E: C®C, который называется тождественным или единичным оператором.
.Получим линейный оператор E: C®C, который называется тождественным или единичным оператором. . Пусть
. Пусть 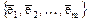 - ортонормированный базис в
- ортонормированный базис в 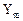 , а
, а 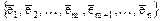 - его расширение до базиса в
- его расширение до базиса в  . Поставим в соответствие каждому вектору
. Поставим в соответствие каждому вектору 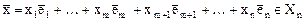 вектор
вектор  , определив его следующим образом
, определив его следующим образом 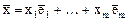 . Полученное отображение – линейный оператор, который называется оператором проектирования на подпространство.
. Полученное отображение – линейный оператор, который называется оператором проектирования на подпространство. и
и 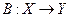 называются равными, если
называются равными, если  .
.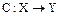 называется суммой операторов
называется суммой операторов 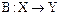 (
(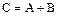 ), если
), если 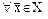
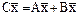 .
.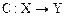 называется произведением оператора
называется произведением оператора 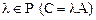 , если
, если 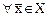
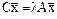 .
. называется произведением операторов
называется произведением операторов  (С=ВА), если
(С=ВА), если 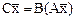 .
.


