Равноточных измерений
Измерения называются равноточными, если они проведены одинаковыми по точности методами, или одним и тем же методом в одинаковых условиях. В результате n измерений некоторой физической величины x, истинное значение которой X0 неизвестно, вследствие наличия случайных погрешностей получается ряд численных значений x1; x2, …, xn, которые в общем случае отличаются друг от друга и от X0. При обработке результатов этих измерений возникают две задачи: 1. Нахождение по результатам отдельных измерений наилучшей оценки истинного значения, т.е. значения, наиболее близкого к истинному; 2. Определение погрешности полученной оценки. Для большого числа практических случаев, когда грубые погрешности (промахи) встречаются редко, а случайные погрешности распределены по нормальному закону, наилучшей оценкой измеряемой величины является среднее арифметическое
Отдельные результаты измерений являются случайными величинами, поскольку содержат случайные погрешности ∆Хi: ∆хi = хi – х0 Среднее арифметическое
также будет случайной. Это говорит о том, что истинное значение абсолютной погрешности найти невозможно, можно лишь тем или иным способом приближенно оценить ее значение. Например, можно считать, что с определенной вероятностью значение абсолютной погрешности по абсолютной величине будет меньше некоторой заданной величины
Отсюда следует, что истинное значение измеряемой величины с вероятностью
Интервал Таким образом, для характеристики случайной погрешности необходимо знать два числа, а именно – величину оценки абсолютной погрешности В качестве ширины доверительного интервала можно взять
Среднее арифметическое имеет меньшее рассеивание и соответственно его среднеквадратичная погрешность будет меньше в
В физических, биологических, медицинских, физиологических и др. измерениях обычно пользуются значениями доверительной вероятности
где Если взять величину абсолютной погрешности Наряду со среднеквадратичной погрешностью
Все приведенные выше результаты теории случайных погрешностей применимы для характеристики точности измерения лишь в случае, если измерение многократно повторено. Последовательность действий при оценке истинного значения измеряемой величины и оценки случайной погрешности следующая: 1. находится среднее арифметическое по результатам измерений:
2. находится оценка среднеквадратической погрешности отдельного результата измерения:
3. находится максимальная абсолютная погрешность отдельного измерения:
4. проверяется, все ли результаты измерений укладываются в интервал 5. находится среднеквадратическая погрешность среднего арифметического:
6. находится из таблицы коэффициент
7. записывается результат измерения:
при заданном 8. если необходимо, то находится относительная погрешность, при этом, поскольку Х0 неизвестно, приближенно его заменяют на
|

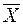 отдельных результатов измерения:
отдельных результатов измерения: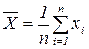 (7)
(7)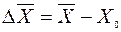
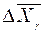 , т.е.
, т.е.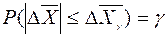 . (8)
. (8)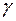 накрывается интервалом
накрывается интервалом 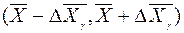 , т.е.
, т.е. 
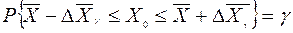 . (9)
. (9)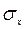 - среднеквадратичную погрешность или ее оценку Sx. Для отдельного измерения она равна:
- среднеквадратичную погрешность или ее оценку Sx. Для отдельного измерения она равна: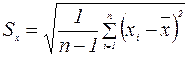 . (10)
. (10)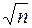 раз.
раз.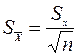 . (11)
. (11)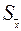 , т.е.:
, т.е.: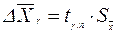 , (12)
, (12)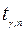 - коэффициент, зависящий от величины доверительный вероятности
- коэффициент, зависящий от величины доверительный вероятности 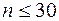 интервал
интервал  , то вероятность того, что доверительный интервал
, то вероятность того, что доверительный интервал 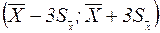 содержит Х0 будет равна
содержит Х0 будет равна 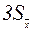 невозможно. Это правило известно под названием “правила трех сигм”.
невозможно. Это правило известно под названием “правила трех сигм”.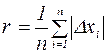 . (13)
. (13)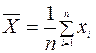 , (14)
, (14) , (15)
, (15)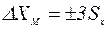 , (16)
, (16)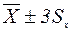 , если да, то переходим к следующему пункту, если нет, то такое значение отбрасыватся (тем самым мы избавляемся от промахов) и вычисления следует начать сначала.
, если да, то переходим к следующему пункту, если нет, то такое значение отбрасыватся (тем самым мы избавляемся от промахов) и вычисления следует начать сначала.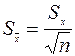 (17)
(17)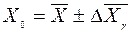 (19)
(19)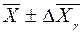 накрывает
накрывает 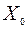 , т.е.
, т.е. 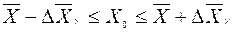 .
.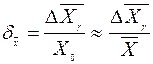 . (20)
. (20)


