Определение интеграла Джоуля и термически эквивалентного тока короткого замыкания
Количественную оценку степени термического воздействия тока КЗ на проводники и электрические аппараты обычно производят с помощью интеграла Джоуля
где: Количественную оценку степени термического воздействия тока КЗ можно также производить с помощью термически эквивалентного тока КЗ
Интеграл Джоуля допускается определять приближенно как сумму интегралов от периодической и апериодической составляющих тока КЗ, т.е.
где: Интеграл Джоуля (и соответственно термически эквивалентный ток КЗ) является сложной функцией параметров источников энергии (генераторов, синхронных компенсаторов, электродвигателей), конфигураций исходной расчетной схемы, положения расчетной точки КЗ относительно источников энергии, ее удаленности от последних и других факторов. Поэтому рекомендуемая методика аналитических расчетов интеграла Джоуля (термически эквивалентного тока КЗ) предусматривает учет особенностей расчетной схемы. Предварительно по исходной расчетной схеме составляют эквивалентную схему замещения, в которой, как и при расчете начального значения периодической составляющей тока КЗ, все синхронные и асинхронные машины представляют сверхпереходными сопротивлениями и сверхпереходными ЭДС, приведенными к базисной ступени напряжения или выраженными в относительный единицах при выбранных базисных условиях. Затем эту схему преобразуют в простейшую схему, вид которой зависит от исходный условий, т. е. от наличия или отсутствия вблизи расчетной точки КЗ отдельного источника энергии и его вида. Наконец, в зависимости от полученной простейшей схемы по одной из приведенных ниже формул определяют интеграл Джоуля или термически эквивалентный ток КЗ. Если исходная расчетная схема имеет произвольный характер, но для всех генераторов (синхронных компенсаторов, синхронных и асинхронных электродвигателей) расчетное КЗ является удаленным, т. е. отношение действующего значения периодической составляющей тока любого генератора в начальный момент КЗ к его номинальному току не достигает двух, то путем преобразования все генераторы и источники энергетической системы следует за источником, ЭДС которого считать неизменной по амплитуде, а индуктивное сопротивление равным результирующему эквивалентному сопротивлению Хс расчетный схемы (рисунок 12.1, а).
Рисунок 12.1. Простейшие схемы замещения (а…г), соответствующие различным исходным расчетным схемам При этом интеграл Джоуля определяется по формуле
где: Термически эквивалентный ток КЗ в рассматриваемом случае составляет
В тех случаях, когда
Если исходная расчетная схема содержит один или несколько однотипных генераторов (синхронных компенсаторов), причем последние находятся в одинаковых условиях относительно расчетной точки КЗ (все машины или блоки присоединены к общим шинам), а расчетное КЗ является близким, т.е. действующее значение периодической составляющей тока генератора в начальный момент КЗ превышает его номинальный ток в два и более раза, то исходную схему замещения также преобразуют в простейшую схему, содержащую результирующее эквивалентное сопротивление Xг и эквивалентную ЭДС Ег (рис 9.1, б), однако амплитуда этой ЭДС изменяется во времени. В этом случае интеграл Джоуля определяют по формуле
где: Относительный интеграл Джоуля
где:
|

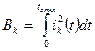
 - ток КЗ в произвольный момент времени
- ток КЗ в произвольный момент времени  , А;
, А; 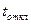 - расчетная продолжительность КЗ, с.
- расчетная продолжительность КЗ, с. , т.е. неизменного по амплитуде (синусоидального) тока, который за время, равное расчетной продолжительности КЗ, оказывает на проводник или электрический аппарат такое же термическое воздействие, как и реальный ток КЗ за это же время. Этот ток связан с интегралом Джоуля простым соотношением
, т.е. неизменного по амплитуде (синусоидального) тока, который за время, равное расчетной продолжительности КЗ, оказывает на проводник или электрический аппарат такое же термическое воздействие, как и реальный ток КЗ за это же время. Этот ток связан с интегралом Джоуля простым соотношением .
.
 - интеграл Джоуля от периодической составляющей тока КЗ;
- интеграл Джоуля от периодической составляющей тока КЗ; 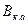 интеграл Джоуля от апериодической составляющей тока КЗ.
интеграл Джоуля от апериодической составляющей тока КЗ.
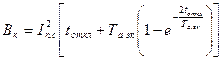
 - действующее значение периодической составляющей тока КЗ от эквивалентного источника энергии (системы), А;
- действующее значение периодической составляющей тока КЗ от эквивалентного источника энергии (системы), А;  - эквивалентная постоянная времени затухания апериодической составляющей тока КЗ, с.
- эквивалентная постоянная времени затухания апериодической составляющей тока КЗ, с.
 , интеграл Джоуля и термически эквивалентный ток КЗ можно определять по более простым формулам:
, интеграл Джоуля и термически эквивалентный ток КЗ можно определять по более простым формулам: ;
; 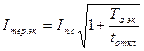
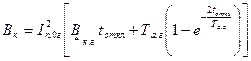
 - действующее значение периодической составляющей тока генератора в начальный момент КЗ, А;
- действующее значение периодической составляющей тока генератора в начальный момент КЗ, А;  - постоянная времени затухания апериодической составляющей тока КЗ от генератора, с;
- постоянная времени затухания апериодической составляющей тока КЗ от генератора, с;  относительный интеграл Джоуля.
относительный интеграл Джоуля.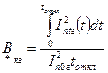
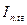 - действующее значение периодической составляющей тока генератора в произвольный момент КЗ, А.
- действующее значение периодической составляющей тока генератора в произвольный момент КЗ, А.


