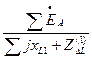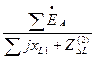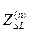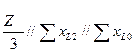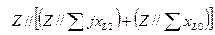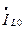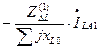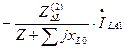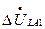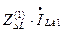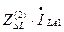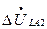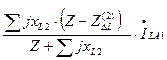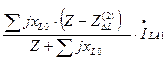Разрыв одной фазы трехфазной цепи.
Разрыв одной фазы можно характеризовать граничными условиями
т.е. они аналогичны граничным условиям двухфазного короткого замыкания на землю. При разложении на симметричные составляющие условия приводят к равенствам
Для тока прямой последовательности фазы «А» в месте разрыва получим
Полученные аналогично
Для определения напряжений с одной стороны продольной симметрии следует предварительно найти по схемам отдельных последовательностей симметричной части цепи соответствующие составляющие этих напряжений. Прибавив к последним
Таблица 15.3. Симметричные составляющие токов и падений напряжений в месте однократной продольной несимметрии
Рекомендуемая литература: ОЛ2, ОЛ3 Контрольные вопросы 1. Укажите основные положения метода симметричных составляющих. 2. К чему сводится расчёт несимметричных режимов при использовании метода симметричных составляющих? 3. Как определяются сопротивления прямой, обратной и нулевой последовательностей для элементов СЭС? 4. Какие виды КЗ относят к поперечной несимметрии? 5. Как определить токи и напряжения при различных видах поперечной несимметрии? 6. Правило эквивалентности прямой последовательности. 7. Каковы соотношения между токами различных видов поперечной несимметрии? 8. Какие виды повреждений относят к продольной несимметрии? 9. Какой вид имеют комплексные схемы замещения при продольной несимметрии? 10. Как формулируется правило эквивалентности прямой последовательности при продольной несимметрии? 11. Какова последовательность расчёта токов в неповреждённых фазах при продольной несимметрии?
|

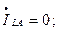
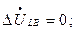
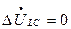
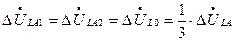
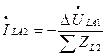 ,
, 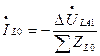
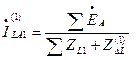 .
.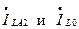 приведены в таблице 15.3.
приведены в таблице 15.3.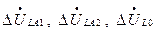 , находят симметричные составляющие напряжений с другой стороны продольной несимметрии. Зная симметричные составляющие токов и напряжений (таблица 15.3), можно, используя выражения, получить фазные величины токов и напряжений.
, находят симметричные составляющие напряжений с другой стороны продольной несимметрии. Зная симметричные составляющие токов и напряжений (таблица 15.3), можно, используя выражения, получить фазные величины токов и напряжений.