Учет переходного сопротивления в месте замыкания
При коротких замыканиях переходное сопротивление в основном определяется сопротивлением электрической дуги, которое в первом приближении можно считать активным сопротивлением На рисунке 15.4 приведены схемы несимметричных коротких замыканий с учетом сопротивления дуги. Здесь двухфазное короткое замыкание через дугу представлено как глухое короткое замыкание на ответвлении, фазы которого имеют одинаковое сопротивление Такие искусственные приемы не нарушают граничных условий и позволяют наиболее просто получить расчетные формулы для токов и напряжений последовательностей и действительных токов и напряжений фаз по аналогии с формулами (таблица 15.1 и 15.2). Для однофазного короткого замыкания через дугу формула для определения тока прямой последовательности имеет вид
Для двухфазного короткого замыкания:
Для двухфазного короткого замыкания на землю:
Рисунок 15.4. Схемы несимметричных коротких замыканий через дугу для двухфазного (а), однофазного (б), двухфазного на землю (в) замыканий Таблица 15.1. Симметричные составляющие токов и напряжений в месте коротких замыканий
Продолжение таблицы 15.1
Примечание. а = - 0,5 + j 0,866, а2 = - 0,5 – j 0,866, а – а2 = j
Таблица 15.2. Значения дополнительного сопротивления
Примечание. Для упрощения записи опущен индекс Однократная продольная несимметрия. Продольную несимметрию в какой-либо точке системы можно представить в общем виде включением в рассечку каждой фазы неодинаковых сопротивлений, причем последние могут быть еще связаны между собой взаимоиндукцией, значения которой для каждой пары фаз также различны. Как отмечалось ранее, такой подход к решению задачи принципиально позволяет получить расчетные выражения для определения токов и напряжений в самом общем виде. Однако значительно проще и нагляднее проводить решение для каждого вида продольной несимметрии, используя характеризующие его граничные условия. При этом, рассматривая только основную гармонику режима, исходят из следующих условий: включение сопротивления в фазу при неизменной ЭДС источника питания тождественно шунтированию таких же сопротивлений в других фазах, шунтирование в фазе тождественно включению такого же сопротивления, но с обратным знаком, разрыв фазы тождественен включению в место разрыва источника напряжения, равного падению напряжения на концах разорванной фазы. Как и для поперечной несимметрии, при расчете продольной несимметрии эффективным является применение метода симметричных составляющих, в соответствии с которым расчетные выражения можно выразить через симметричные составляющие тока и напряжения фазы «А», принятой за основную (особую).
где Токи определенных последовательностей вызывают падения напряжения соответствующих последовательностей. Эта взаимосвязь их описывается системой независимых уравнений
где Таким образом, как и при поперечной несимметрии, методика получения расчетных соотношений основывается на решении системы уравнений с учетом граничных условий, характеризующих несимметрию. В настоящем разделе рассмотрены два вида наиболее часто встречающейся продольной несимметрии: разрыв одной фазы и разрыв двух фаз (в одном и том же месте). Реальная схема с однократной продольной несимметрией приводится к схемам замещения без разрыва. Это достигается введением в месте повреждения источника продольного напряжения, имеющего значение, равное падению напряжения в месте продольной несимметрии. В электрической системе могут возникать одновременно поперечная и продольная несимметрии в разных комбинациях, которые приводят к сложным видам повреждений. В этом случае последовательность вычислительных операций повторяется в каждой точке несимметрии.
|


 . В схему однофазного короткого замыкания в каждую фазу введены одинаковые сопротивления
. В схему однофазного короткого замыкания в каждую фазу введены одинаковые сопротивления 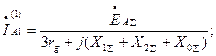




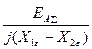





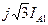
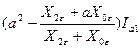
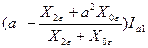
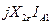

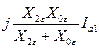
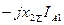
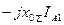


 , а2 – а = - j
, а2 – а = - j 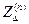 и коэффициента m(n)
и коэффициента m(n)

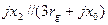
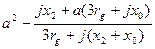



 у величин
у величин  , которые являются соответствующими результирующими сопротивлениями относительно места короткого замыкания.
, которые являются соответствующими результирующими сопротивлениями относительно места короткого замыкания.
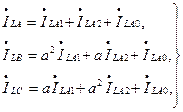
 – токи и падения напряжения для несимметричной системы фазных величин А, В и С;
– токи и падения напряжения для несимметричной системы фазных величин А, В и С;  – симметричные составляющие токов и падений напряжения прямой, обратной и нулевой последовательностей.
– симметричные составляющие токов и падений напряжения прямой, обратной и нулевой последовательностей.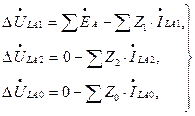
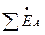 – суммарная ЭДС источников питания, имеющая место только в схеме прямой последовательности;
– суммарная ЭДС источников питания, имеющая место только в схеме прямой последовательности;  – результирующие сопротивления отдельных последовательностей относительно места нарушения продольной несимметрии.
– результирующие сопротивления отдельных последовательностей относительно места нарушения продольной несимметрии.


