Переходные процессы в цепи R, L при воздействии источника синусоидальной ЭДС
В момент времени t = 0 цепь, состоящая из катушки индуктивности с параметрами R и L, подключается к источнику синусоидальной ЭДС
Начальная фаза
Уравнение по второму закону Кирхгофа:
или
Характеристическое уравнение имеет вид:
Корень этого уравнения Переходный ток в цепи состоит из суммы принуждённой и свободной составляющих:
Свободная составляющая не зависит от формы действующей в цепи ЭДС и записывается так же, как и в предыдущих задачах:
Принуждённая составляющая по форме совпадает с формой приложенного напряжения, т.е. является синусоидальной функцией времени, и её удобнее всего рассчитывать комплексным методом:
где Z – модуль комплексного сопротивления, Мгновенное значение принуждённой составляющей
Таким образом, переходный ток в цепи
Постоянная А определяется при
Величина тока
так как до коммутации ток в цепи был равен нулю. Следовательно,
Ток переходного процесса
Если коммутация происходит при Если коммутация происходит при
|
.
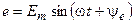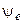в такого рода задачах соответствует моменту коммутации t = 0.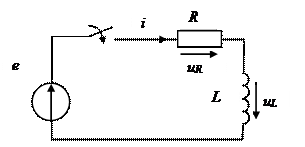
,
.
.
.
.
.
,
; 
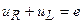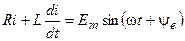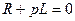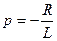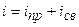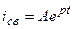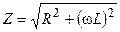– аргумент комплексного сопротивления,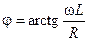 
.
.
.
:
.
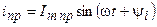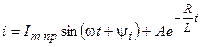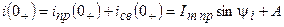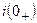вычисляется, используя первый закон коммутации:
,
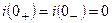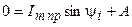, откуда 
.
.
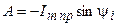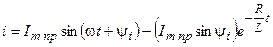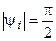, то начальное значение тока 
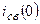максимально и равно 
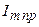, и переходный ток достигает экстремума в конце первого полупериода.
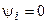, то в цепи сразу наступает установившийся режим без переходного процесса.
