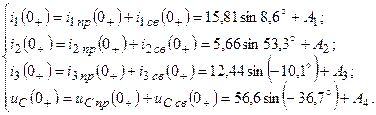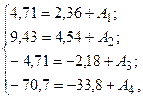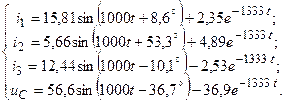Свободные составляющие.
Определим корень характеристического уравнения, полученного через входное сопротивление. Входное комплексное сопротивление схемы (см. рис.3) для послекоммутационного состояния
Заменим
Корень полученного характеристического уравнения
Так как корень единственный, то свободные составляющие записываем в следующей форме:
Для определения постоянных А 1, А 2, А 3, А 4 необходимо вычислить начальные значения Решаем систему алгебраических уравнений
Здесь Подставив числовые значения параметров, получим
Решение этой системы даёт
Для момента времени
После подстановки левых частей получим:
откуда А 1 = 2,35; А 2 = 4,89; А 3 = – 2,53; А 4 = – 36,9. Окончательное решение задачи имеет вид:
|

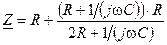 .
.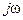 на p и приравняем полученный результат нулю:
на p и приравняем полученный результат нулю: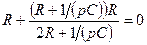 ,
,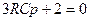 .
.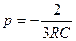 ,
, 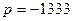 с-1.
с-1.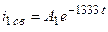 ;
; 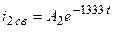 ;
; 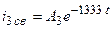 ;
; 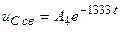 .
.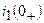 ,
, 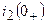 ,
, 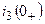 ,
, 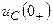 .
.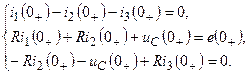
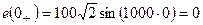 ,
, 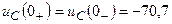 В.
В.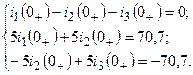
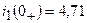 А;
А; 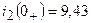 А;
А; 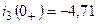 А.
А. получим следующую систему уравнений:
получим следующую систему уравнений: