Установившийся режим до коммутации.
Имеет место установившийся режим синусоидальных токов (рис.2). Ветвь с током Расчёт проводим комплексным методом. Учитывая равенство
Комплексная амплитуда напряжения на ёмкостном элементе
Мгновенное значение этого напряжения
Для момента времени
Определение других токов и напряжений на данном этапе не требуется, так как они не используются в дальнейшем для определения начальных условий при
2. Дифференциальные уравнения с момента времени
3. Принуждённые составляющие находим из системы уравнений для комплексных амплитуд, описывающей установившийся синусоидальный режим после переходного процесса (рис. 3):
После подстановки числовых значений система имеет вид:
Решение этой системы даёт значения комплексных амплитуд:
Запишем мгновенные значения принуждённых составляющих:
Вычислить принуждённые составляющее можно также используя любой из методов расчёта установившихся режимов в цепях синусоидального тока: эквивалентных преобразований, контурных токов, узловых потенциалов.
|

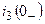 разомкнута и схема содержит только один контур.
разомкнута и схема содержит только один контур.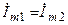 , комплексная амплитуда тока в контуре по закону Ома
, комплексная амплитуда тока в контуре по закону Ома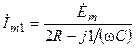 ;
; 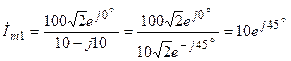 А.
А.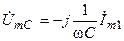 ;
; 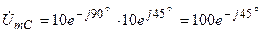 В.
В.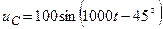 В.
В.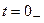 :
: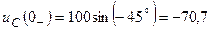 В.
В.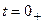 . Для цепи с индуктивностью необходимо определить ток
. Для цепи с индуктивностью необходимо определить ток 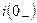 в ветви с индуктивным элементом.
в ветви с индуктивным элементом.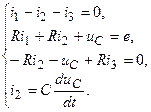
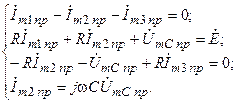
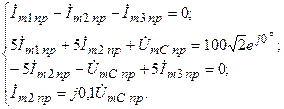
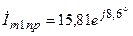 А;
А; 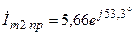 А;
А; 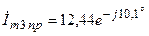 А;
А; 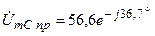 В.
В.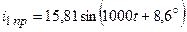 А;
А; 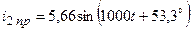 А;
А; 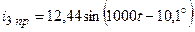 ;
; 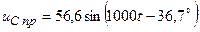 В.
В.


