Рациональные дроби
Под целой рациональной функцией подразумевается многочлен п- й степени f (x) = a 0 x n + a 1 x n – 1+ a 2 x n – 2 +¼+ an,(1) где а 0 ¹ 0 и п ³ 0. Дробно-рациональная функция или рациональная дробь – это частное двух целых рациональных функций Рациональная дробь называется несократимой, если её числитель взаимно прост со знаменателем. Теорема. Всякая рациональная дробь равна некоторой несократимой дроби, определяемой однозначно с точностью до множителя нулевой степени, общего для числителя и знаменателя. Доказательство. Всякую рациональную дробь можно сократить на наибольший делитель её числителя и знаменателя, после чего будет получена равная ей несократимая дробь. Если равны друг другу несократимые дроби
то из взаимной простоты f (x) и g (x) следует, что j(х) делится на f (x), а из взаимной простоты g (x) и y (х) следует, что f (x) делится на j(х). Отсюда f (x) = сj(х), а тогда из (2) следует g (x) = сy (х). Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя. Будем считать, что многочлен степени 0 является правильной дробью. Теорема. Всякая рациональная дробь представима притом единственным способом, в виде суммы многочлена и правильной дроби. Пусть дана рациональная дробь f (x)/ g (x). Если, деля числитель на знаменатель, получим равенство f (x) = q (x) g (x) + r (x), где степень r (x) меньше степени g (x), то очевидно,
Если также справедливо равенство
где степень j(х) меньше степени y (х), то справедливо равенство
Так как слева стоит многочлен, а справа – правильная дробь, то обязательно q (x) = q 1(x) и
Из изложенного ранее следует, что среди многочленов с действительными коэффициентами и со старшим коэффициентом 1, неразложимыми на множители меньшей степени, или неприводимыми, являются лишь линейные многочлены вида х – а и квадратные многочлены вида
(конечно, здесь Правильная рациональная дробь f (x)/ g (x) называется простейшей, если её знаменатель g (x) является степенью неприводимого многочлена р (х), g (x) = рk (х), k ³ 1, а степень числителя f (x) меньше степени р (х). Основная теорема о рациональных дробях. Всякая правильная рациональная дробь разлагается в сумму простейших дробей. Рассмотрим сначала правильную рациональную дробь g (x) u 1(х) + h (х) v 1(x) = 1 Отсюда g (x)[ u 1(х) f (x)] + h (х)[ v 1(x) f (x)] = f (x) (3) Пусть остаток от деления произведения u 1(х) f (x) на h (х) равен u (х), степень которого меньше степени h (х). Тогда равенство (3) можно переписать в виде g (x) u (х) + h (х) v (x) = f (x), (4) где многочлен v (x) легко определяется. Так как степень произведения g (x) u (х) меньше степени произведения g (x) h (х), и степень f (x) меньше степени произведения g (x) h (х) по условию теоремы, то и произведение h (х) v (x)имеет степень, меньшую, чем g (x) h (х). Поэтому степень v (x) меньше степени g (x). Из (3) следует равенство
в правой части которого стоит сумма правильных дробей. Если хотя бы одни из знаменателей g (x) или h (х) разлагается в произведение взаимно простых множителей, то можно провести дальнейшее разложение. Отсюда следует, что всякая правильная дробь разлагается в сумму нескольких правильных дробей, каждая из которых имеет знаменателем степень некоторого неприводимого многочлена. Если дана правильная дробь f (x)/ g (x), знаменатель которой разлагается на неприводимые множители
(конечно, всегда можно считать, что старший коэффициент знаменателя рациональной дроби равен единице), причём pi (х) ¹ pj (x) при i ¹ j, то
Все слагаемые в правой части этого равенства являются правильными дробями. Рассмотрим правильную дробь вида u (х)/ рk (x), где р (х) – неприводимый многочлен. Разделим u (х) на рj (x), где j – наибольшее натуральное число из тех, при которых можно осуществлять деление u (х) на рj (x) (j £ k – 1). Отметим, что при степени многочлена и (x) равной т, если р (x) = х – а, то j = т. Если же р (x) = х 2 + рх + q (p 2 – 4 q < 0), то при т чётном j = т/ 2, а при т нечётном j = (т - 1 )/ 2. Полученный остаток разделим на рj- 1(x) и т. д. В результате придём к равенствам
¼¼
При этом степень u (х) по условию меньше степени рk (x), а степень каждого из остатков ui (х) i = 1,2,¼, j + 1 меньше степени соответствующего делителя рj–i +1(x), то степени всех частных s 1(x), s 2(x),…, sj+ 1(x) будут строго меньше степени многочлена р (х).
Отсюда получается искомое представление рациональной дроби u (х)/ рk (x) в виде суммы простейших дробей:
и основная теорема доказана. Теорема единственности. Всякая правильная рациональная дробь обладает единственным разложением в сумму простейших дробей. Пусть некоторая правильная рациональная дробь может быть представлена в виде суммы простейших дробей двумя способами. Вычитая одно из этих представлений из другого и приводя подобные члены, получим сумму простейших дробей, тождественно равную нулю. Пусть знаменатели простейших дробей, составляющих эту сумму, будут некоторыми степенями различных неприводимых многочленов р 1(х), р 2(х),¼, рs (х) и пусть наивысшая степень многочлена рi (х), i = 1,2,¼, s, являющегося одним из этих знаменателей, будет
|

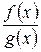 . Будем рассматривать рациональные дроби с действительными коэффициентами.
. Будем рассматривать рациональные дроби с действительными коэффициентами. , то есть
, то есть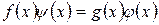 , (2)
, (2)
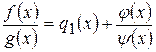 ,
,
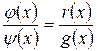

 – комплексно сопряженные числа)
– комплексно сопряженные числа) , где многочлены g (x) и h (х) взаимно просты. Тогда существуют многочлены u 1(х) и v 1(x), такие что
, где многочлены g (x) и h (х) взаимно просты. Тогда существуют многочлены u 1(х) и v 1(x), такие что ,
,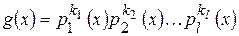

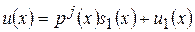


 .
. ,
, . Умножим обе части рассматриваемого равенства на произведение
. Умножим обе части рассматриваемого равенства на произведение  . Все слагаемые полученной суммы, кроме одного, превратятся при этом в многочлены. Слагаемое
. Все слагаемые полученной суммы, кроме одного, превратятся при этом в многочлены. Слагаемое  превратится в дробь
превратится в дробь 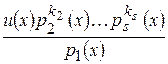 . Знаменатель этой дроби не является делителем числителя, так как многочлен р 1(x) неприводим, а все множители числителя с ним взаимно просты. Выполняя деление числителя на знаменатель с остатком, в результате получим, что равна нулю сумма многочлена и отличной от нуля правильной дроби, что невозможно.
. Знаменатель этой дроби не является делителем числителя, так как многочлен р 1(x) неприводим, а все множители числителя с ним взаимно просты. Выполняя деление числителя на знаменатель с остатком, в результате получим, что равна нулю сумма многочлена и отличной от нуля правильной дроби, что невозможно.


