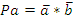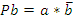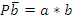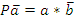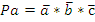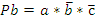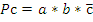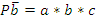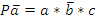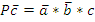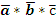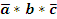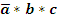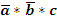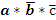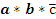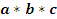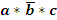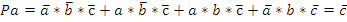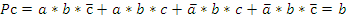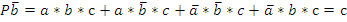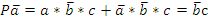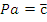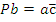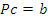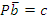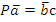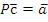Законы алгебры логики.
Алгебра логики подчиняется ка общим законам алгебры так имеет и некоторые специальные. Общие: Переместительнный: a+b=b+a, a*b=b*a. Сочетательный: a*(b*c)=(a*b)*c, (a+b)+c=a+(b+c). Распределительный: a*(b+c)=a*b+a*c. Специальные: закон множеств закон тавтологии закон дополнительности Закон множеств: 1) 0*а*а*...=0 Если один из сомножителей функций является ложью то функция обращается в 0. 2) 0+а+а+...=а Дизъюнкция 0 и а определяется переменной. 3) 1*а*а*а...=а Конъюнкция истины определяется переменной 4) 1+а+а+...=1 Дизъюнкция истины всегда истина. Закон тавтологии: 1) а*а*а*...*а=аn=а 2) а+а+а+...а=n*a=a Истина повторенная сколько угодно раз всегда остается истиной. Закон дополнительности: 1 Следствие: а*а-=0. Конъюнкция истины и ее инверсии всегда ложь. 2 Следствие: а+а-=1. Дизъюнкция истины и ее инверсии всегда истина.
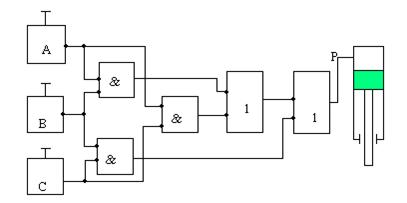
29 Синтез логических схем управления методом алгебры логики. Составим логическую схему управления прессом штоссель которого срабатывает при нажатии как минимум двух кнопок из трех.
P=a*b*c-+a*b-*c+a-*b*c+a*b*c «И»ѕ8 элементов «ИЛИ»ѕ3 элемента «НЕ»ѕ3 элемента ВСЕГОѕ14 элементов. Любая логическая функция управления должна быть подвергнута минимизации. Существуют различные методы минимизации. Метод минимизации посредством карт Карно. Карта Карноѕэто таблица состоящая из ячеек, количество ячеек определяется по формуле: N=2k, где kѕколичество участвующих в функции переменных. В ячейках записываются варианты состояний. Две соседние ячейки отличаются только одной переменной.
Некоторые функции можно минимизировать методом непосредственного упрощения, без карт Карно. Используя закон тавтологии, добавим комбинацию abc 2 раза: a*b*c-+a*b-*c+a-*b*c+a*b*c+a*b*c+a*b*c=(a*b*c-+a*b*c)+(a*b-*c+ a*b*c)+(a-*b*c+a*b*c)= =a*b*(c+c-)+b*c*(a+a-)+a*c*(b+b-). Этот метод неочевиден и весьма трудоемок. Аналогичное преобразование выполним с использованием карт Карно. Эталонная карта повторяется. В ячейки, соответствующим реализованным сочетаниям, записывается «1». Единица объединяется в прямоугольные контуры. Количество единиц определяется по формуле 2n (2,4,8,16...), а единица может входить в любой контур. Так как две соседние ячейки всегда отличаются только одной переменной и эта переменная незначимая и ее можно опустить.
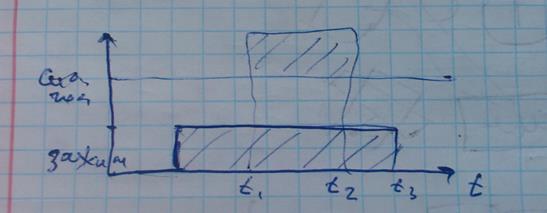
30. Синтез логической схемы управления операцией на АЛ. Теория релейной автоматики была придумана для дискретных устройств (реле, концевые выключатели). В современных условиях многие функции релейной автоматики взяли на себя компьютеры. Сегодня релейная автоматика – это язык программирования компьютера или контроллеров, т.е. текстовая запись логических функций управления, как результат анализа входных переменных. Суть задачи: Спроектировать систему управления операцией сверления на агрегатном станке.
Пусть зажим заготовки осуществляется логической функцией Pa, соответственно Состояние исполнительных элементов контролируется концевыми выключателями. Концевой выключатель a – заготовка зажата Концевой выключатель Концевой выключатель b – заготовка просверлена Концевой выключатель Запишем логические функции на всех тактах работы станка 1. Зажать заготовку
2. Сверление
3. Заготовка просверлена
4. Разжать заготовку
Нельзя допускать многотактность САУ. Для сведения моноготактных САУ к однотактным вводят элементы памяти (триггеры). Перепишем тактограмму с элементом с (триггер). 1. 2. 3. 4. 5. 6. Мы избавились от многотактности. Минимизация шести логических функций управления.
1) Ячейки бывают обязательные 2) Ячейки бывают запрещённые 3) Неиспользованные ячейки (используем по своему усмотрению) 4) Безразличные 1) Зажимай заготовку, пока триггер выключен. 2) Сверли, когда заготовка зажата и триггер выключен. 3) Включи триггер, когда заготовка просверлена 4) Отводи сверло, когда триггер включен 5) Разжимай, когда силовая головка отведена и триггер включен 6) Выключай триггер, когда заготовка разжата 1. 2. 3. 4. 5. 6.
|

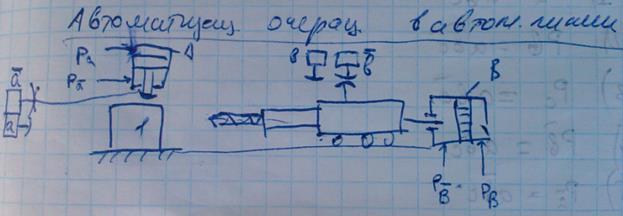
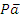 –разжим заготовки, сверление Pb, отвод
–разжим заготовки, сверление Pb, отвод 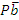
 - разжата
- разжата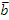 - сигнал головка отведена
- сигнал головка отведена