Решение. Так как степень многочлена в числителе меньше степени многочлена в знаменателе, то производить деление нам не придется
Так как степень многочлена в числителе меньше степени многочлена в знаменателе, то производить деление нам не придется. Переходим к разложению знаменателя на множители. Для начала выносим х за скобки.
Находим корни квадратного трехчлена
Следовательно, квадратный трехчлен можно записать как То есть, знаменатель примет вид При данном знаменателе, исходная дробь раскладывается в сумму трех простейших дробей первого типа с неопределенными коэффициентами:
Полученную сумму приводим к общему знаменателю, но в числителе при этом скобки не раскрываем и не приводим подобные при А, В и С (на этом этапе как раз отличие от метода неопределенных коэффициентов):
Таким образом, пришли к равенству:
А теперь, для нахождения неопределенных коэффициентов, начинаем подставлять в полученное равенство «частные значения», при которых знаменатель обращается в ноль, то есть х=0, х=2 и х=3 для нашего примера: При х=0 имеем:
При х=2 имеем:
При х=3 имеем:
Ответ:
Рассмотрим пример.
Разложить дробно рациональное выражение
|
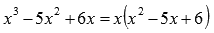
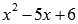(например, по теореме Виета):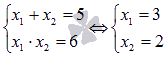
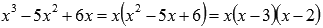
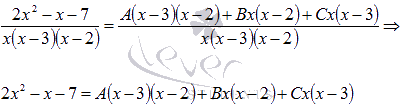
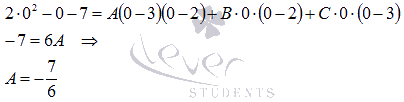
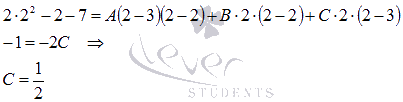
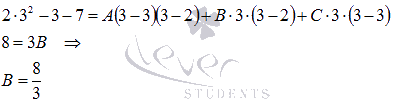
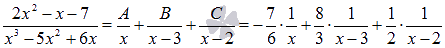
на простейшие дроби.
