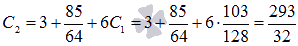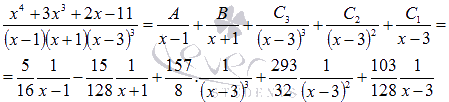Решение. Так как степень многочлена числителя меньше степени многочлена знаменателя и знаменатель уже разложен на множителиТак как степень многочлена числителя меньше степени многочлена знаменателя и знаменатель уже разложен на множители, то исходное выражение представится в виде суммы простейших дробей следующего вида:
Приводим к общему знаменателю:
Приравниваем числители.
Очевидно, что нулями знаменателя являются значения х=1, х=-1 и х=3. Используем метод частных значений. При х=1 имеем:
При х=-1 имеем:
При х=3 имеем:
Осталось найти неизвестные Для этого подставляем найденные значения в равенство числителей:
После раскрытия скобок и приведения подобных слагаемых при одинаковых степенях х приходим к равенству двух многочленов:
Приравниваем соответствующие коэффициенты при одинаковых степенях, тем самым составляем систему уравнений для нахождения оставшихся неизвестных
Из первого уравнения сразу находим В итоге получаем разложение на простейшие дроби:
Если бы мы сразу решили применить метод неопределенных коэффициентов, то пришлось бы решать систему пяти линейных алгебраических уравнений с пятью неизвестными. Применение метода частных значений позволило легко отыскать значения трех неизвестных из пяти, что значительно упростило дальнейшее решение.
|
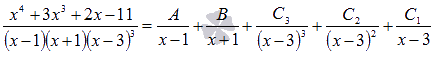
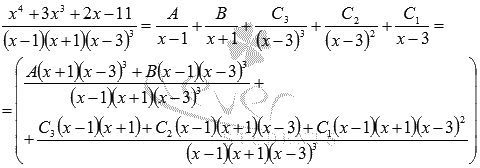
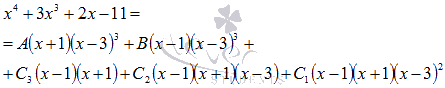
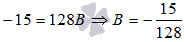
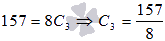
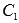и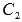 
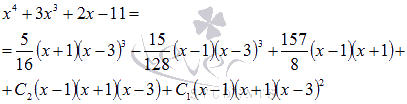
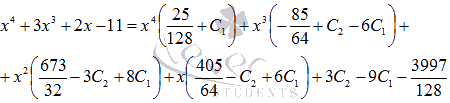
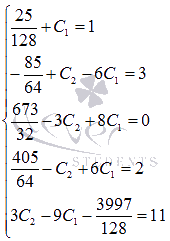
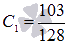, из второго уравнения 
