Разложение дроби на простейшие.
Для начала разберем теорию, далее решим парочку примеров для закрепления материала по разложению дробно рациональной функции на сумму простейших дробей. Подробно остановимся на методе неопределенных коэффициентов и методе частных значений, а также на их комбинации. Простейшие дроби часто называют элементарыми дробями. Различают следующие виды простейших дробей:
где A, M, N, a, p, q – числа, а дискриминант знаменателя в дробях 3) и 4) меньше нуля. Называют их соответственно дробями первого, второго, третьего и четвертого типов.
Приведем математическую аналогию. Часто приходится заниматься упрощением вида выражения, чтобы можно было проводить какие-то действия с ним. Так вот, представление дробно рациональной функции в виде суммы простейших дробей примерно то же самое. Применяется для разложения функций в степенные ряды, ряды Лорана и, конечно же, для нахождения интегралов. К примеру, требуетя взять интеграл от дробно рациональной функции
Но об интегралах в другом разделе.
Разложить дробь
|

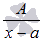
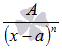
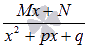

 . После разложения подынтегральной функции на простейшие дроби, все сводится к достаточно простым интегралам
. После разложения подынтегральной функции на простейшие дроби, все сводится к достаточно простым интегралам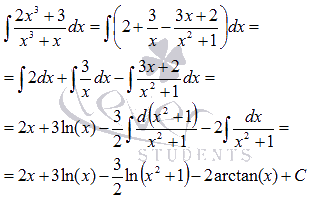
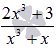 на простейшие.
на простейшие.


