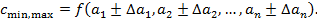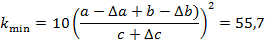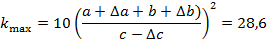Расчёт погрешностей косвенных измерений
Пусть известны две независимо измеренных физических величины 1. Абсолютная погрешность суммы (разности) есть сумма абсолютных погрешностей. То есть, если
то
Более разумная (учитывающая то, что величины
На всех школьных олимпиадах допускается применение любой из этих двух формул. Аналогичные формулы справедливы для случая нескольких (более двух) слагаемых. Таким образом, в результате сложения двух величин сначала вычисляется абсолютная погрешность величины, а после этого может быть вычислена относительная погрешность. Пример: Пусть величина Тогда
2. Относительная погрешность произведения (частного) есть сумма относительных погрешностей. То есть, если
то
Как и в предыдущем случае, более разумной будет формула
Аналогичные формулы справедливы для случая нескольких (более двух) множителей. Таким образом, в результате сложения двух величин сначала вычисляется абсолютная погрешность величины, а после этого может быть вычислена относительная погрешность. Пример: Пусть величина Тогда
3. Правило для возведения в степень. Если Пример: Пусть Тогда
4. Правило умножения на константу. Если Пример: Пусть Тогда
5. Более сложные функции величин разбиваются на более простые вычисления, погрешности которых можно рассчитать по формулам представленным выше. Пример: Пусть Тогда
6. Если расчётная формула сложна и не сводиться к описанным выше случаем, то, школьники знакомые с понятием частной производной могут найти погрешность косвенного измерения следующим образом: пусть
или более простой оценкой:
Пример: Пусть Тогда
7. Школьники, не знакомые с производными, могут пользоваться методом границ, который состоит в следующем: пусть нам известно, что
За абсолютную погрешность величины
Пример: Пусть Тогда
|

 и
и 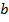 с погрешностями
с погрешностями 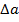 и
и 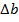 соответственно. Тогда справедливы следующие правила:
соответственно. Тогда справедливы следующие правила:
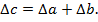
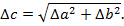
 ,
,  ,
, 
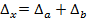
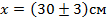
 .
.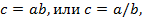
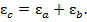

 ,
,  ,
, 

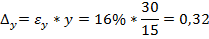
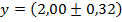
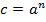 , то
, то  .
.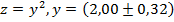



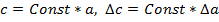 .
.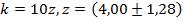
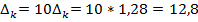
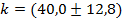
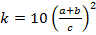
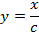
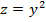
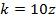
 , тогда
, тогда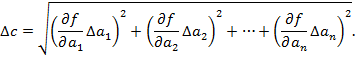
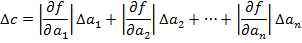
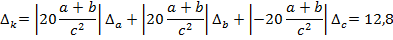
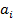 диапазон
диапазон 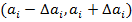 в котором лежит её истинное значение. Рассчитаем минимальное и максимальное возможное значение величины
в котором лежит её истинное значение. Рассчитаем минимальное и максимальное возможное значение величины 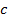 на области задания величин
на области задания величин