Абсолютные и относительные погрешности
Оценка погрешностей
Участникам школьных физических олимпиад высокого уровня (например, третьего или чётвертого этапа всероссийской олимпиады школьников по физике) приходится решать не только теоретические, но и практические задачи. При подготовке к экспериментальному туру олимпиады полезно повторить правила оценки погрешностей измерений, округления и записи конечного результата, потому что на уроках физики этим темам обычно уделяется недостаточно внимания. Абсолютные и относительные погрешности Любая физическая величина может быть измерена лишь с конечной точностью. Насколько бы ни был точным измерительный прибор, результат измерения
Поскольку истинное значение величины обычно заранее неизвестно (иначе зачем проводить измерение?), то и точное значение абсолютной погрешности нельзя определить, а можно лишь оценить. То есть запись в отчёте о проделанном эксперименте Длина нити по сути гласит: «С большой вероятностью истинное значение длины нити лежит в интервале от 36,5 см до 37,5 см.» Обычно при записи результата измерения с абсолютной погрешностью используют знак «
Помимо абсолютной погрешности вводят понятие относительной погрешности, как отношение абсолютной погрешности к результату измерения:
Относительная погрешность величины наиболее наглядно характеризует точность ее измерения.
|

 зачастую не будет совпадать с истинным значением измеряемой величины
зачастую не будет совпадать с истинным значением измеряемой величины 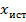 . Поэтому экспериментатор должен не только провести измерение, но и оценить разность
. Поэтому экспериментатор должен не только провести измерение, но и оценить разность  , а также при возможности принять меры по уменьшению этой разницы. Напомним, что разность между найденным на опыте и истинным значением физической величины называется абсолютной погрешностью измерения:
, а также при возможности принять меры по уменьшению этой разницы. Напомним, что разность между найденным на опыте и истинным значением физической величины называется абсолютной погрешностью измерения: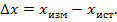
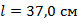 , погрешность
, погрешность 
 » и пишут кратко:
» и пишут кратко: .
.