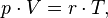Показатель политропы
Кривая на термодинамических диаграммах, изображающая политропный процесс, называется «политропа». Для идеального газа уравнение политропы может быть записано в виде:
где р — давление, V — объем газа, n — «показатель политропы».
В зависимости от вида процесса, можно определить значение n: · Изотермический процесс: · Изобарный процесс: · Адиабатный процесс: · Изохорный процесс: · До сих пор рассматривались процессы, у которых имелись вполне определенные признаки: изохорный процесс осуществлялся при постоянном объеме; изобарный — при постоянном давлении; изотермический — при постоянной температуре; адиабатный— при отсутствии теплообмена между рабочим телом и внешней средой. Наряду с этими процессами можно представить еще бесконечное множество процессов, у которых имеются другие постоянные признаки. · Условились всякий процесс идеального газа, в котором удельная теплоемкость является постоянной величиной, называть политропным процессом, а линию процесса — политропой. · Из определения политропного процесса следует, что основные термодинамические процессы — изохорный, изобарный, изотермический и адиабатный,— если они протекают при постоянной удельной теплоемкости, являются частными случаями политропного процесса. Итак, политропный процесс проходит при постоянной теплоемкости. · · Если теплоемкость зависит от температуры, то нужно найти среднюю теплоемкость, чтобы процесс стал политропным.
ПОЛИТРОПНЫЙ ПРОЦЕСС (политропический процесс) - обратимый термодинамич. процесс при пост. теплоёмкости системы. Линия, изображающая П. п. на термодинамич. диаграмме, наз. политропой. При П. п. кол-во подводимого тепла Изохорический или изохорный процесс — термодинамический процесс, который происходит при постоянном объёме. Для осуществления изохорного процесса в газе или жидкости достаточно нагревать (охлаждать) вещество в сосуде, который не изменяет своего объёма. При изохорическом процессе давление идеального газа прямо пропорционально его температуре (см. Закон Шарля). В реальных газах закон Шарля не выполняется. На графиках изображается линиями, которые называются изохоры. Для идеального газа они являются прямыми во всех диаграммах, которые связывают параметры: T (температура), V (объем) и P (давление).
Первый закон термодинамики в изопроцессах
Здесь U1 и U2 – внутренние энергии газа в начальном и конечном состояниях. Внутренняя энергия идеального газа зависит только от температуры. При изохорном нагревании тепло поглощается газом Q > 0, и его внутренняя энергия увеличивается. При охлаждении тепло отдается внешним телам Q < 0 2. В изобарном процессе (P=const). При изобарном расширении газа подведенное к нему количество теплоты расходуется как на увеличение его внутренней энергии и на совершение работы газом:
При изобарном расширении Q > 0 – тепло поглощается газом, и газ совершает положительную работу. При изобарном сжатии Q < 0 – тепло отдается внешним телам. В этом случае A < 0. Температура газа при изобарном сжатии уменьшается, T2 < T1; внутренняя энергия убывает, ΔU < 0. 3. В изотермическом процессе (T=const). При изотермическом процессе температура газа не изменяется, следовательно, не изменяется и внутренняя энергия газа, ΔU = 0.
Количество теплоты Q, полученной газом в процессе изотермического расширения, превращается в работу над внешними телами. При изотермическом сжатии работа внешних сил, произведенная над газом, превращается в тепло, которое передается окружающим телам. Наряду с изохорным, изобарным и изотермическим процессами в термодинамике часто рассматриваются процессы, протекающие в отсутствие теплообмена с окружающими телами.
То есть газ совершает работу за счет убыли его внутренней энергии. На плоскости (p, V) процесс адиабатического расширения (или сжатия) газа изображается кривой, которая называется адиабатой. При адиабатическом расширении газ совершает положительную работу (A > 0); поэтому его внутренняя энергия уменьшается (ΔU < 0). Это приводит к понижению температуры газа. Вследствие этого давление газа при адиабатическом расширении убывает быстрее, чем при изотермическом расширении. В Формуле мы использовали:
5) Теплоёмкость тела (обычно обозначается латинской буквой C) — физическая величина, определяемая отношением бесконечно малогоколичества теплоты δQ, полученного телом, к соответствующему приращению его температуры δT[1]:
Единица измерения теплоёмкости в Международной системе единиц (СИ) — Дж/К. Теплоёмкость тела (обозначается C) — физическая величина, определяющая отношение бесконечно малого количества теплоты ΔQ, полученного телом, к соответствующему приращению его температуры ΔT: Единица измерения теплоёмкости в системе СИ — Дж/К. Теплоемкость вещества — теплоемкость единицы массы данного вещества. Единицы измерения — Дж/(кг К). Молярная теплоемкость — теплоемкость 1 моля данного вещества. Единицы измерения — Дж/(моль К). Если же говорить про теплоемкость произвольной системы, то ее уместно формулировать в терминах термодинамических потенциалов — теплоемкость есть производная термодинамического потенциала Q по температуре: Понятие теплоёмкости определено как для веществ в различных агрегатных состояниях (твёрдых тел, жидкостей, газов), так и для ансамблей частиц и квазичастиц (в физике металлов, например, говорят о теплоемкости электронного газа). Если речь идёт не о каком-либо теле, а о некотором веществе как таковом, то различают удельную теплоёмкость — теплоёмкость единицы массы этого вещества и молярную — теплоёмкость одного моля его Виды теплоемкости Если ТС – однородное рабочее тело, то в расчетах применяются относительные теплоемкости: - удельная теплоемкость – теплоемкость, отнесенная к 1 кг вещества с=С/m, Дж/кгК; - молярная теплоемкость – теплоемкость, отнесенная с 1 молю вещества - объемная теплоемкость – теплоемкость, отнесенная к 1м3 вещества
Теплоемкость – свойство материала поглощать определенное количество тепла при нагревании и выделять его при охлаждении. Удельная теплоемкость – количество тепла, необходимое для нагревания единицы количества вещества на один градус. Формула для расчёта удельной теплоёмкости (или табл.знач.):
где
В зависимости от единиц измерения количества вещества различают: · массовую теплоемкость С, Дж / (кг К) - это количество теплоты, которое необходимо подвести к единице массы вещества, чтобы нагреть его на единицу температуры; · объемную теплоемкость С’, Дж / (м3 К) - это количество теплоты, которое необходимо подвести к единице объёма вещества, чтобы нагреть его на единицу температуры; · мольную теплоемкость СМ, Дж / (кмоль К) - это количество теплоты, которое необходимо подвести к 1 молю вещества, чтобы нагреть его на единицу температуры 5)Для идеального газа справедливо соотношение Майера:
где Уравнение Майера вытекает из первого начала термодинамики, примененного к изобарному процессу в идеальном газе:
в рассматриваемом случае:
Очевидно, уравнение Майера показывает, что различие теплоёмкостей газа равно работе, совершаемой одним молем идеального газа при изменении его температуры на 1 K, и разъясняет смысл универсальной газовой постоянной МАЙЕРА УРАВНЕНИЕ - ур-ние, устанавливающее связь между теплоёмкостями при пост, давлении Cp и постоянном объёме СV 1кмоля идеального газа: 7) Уравнение Клапейрона-Менделеева. Связь между числом молей газа, его температурой, объемом и давлением. Газы нередко бывают реагентами и продуктами в химических реакциях. Не всегда удается заставить их реагировать между собой при нормальных условиях. Поэтому нужно научиться определять число молей газов в условиях, отличных от нормальных. Для этого используют уравнение состояния идеального газа (его также называют уравнением Клапейрона-Менделеева): PV = nRT где n – число молей газа; P – давление газа (например, в атм; V – объем газа (в литрах); T – температура газа (в кельвинах); R – газовая постоянная (0,0821 л·атм/моль·K). Уравнение Клапейрона - Менделеева (уравнение состояния идеального газа) Это уравнение, связывающее макропараметры между собой. Физика, Билеты по физике за весь школьный курс, Билеты Это уравнение называют уравнением состояния идеального газа (уравнение Менделеева-Клапейрона).
где · · · · Так как
Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона. Уравнение, выведенное Клапейроном, содержало некую неуниверсальную газовую постоянную
Менделеев же обнаружил, что
|


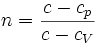 . Здесь
. Здесь  — теплоёмкость газа в данном процессе,
— теплоёмкость газа в данном процессе,  и
и 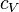 — теплоемкости того же газа, соответственно, при постоянном давлении и объеме.
— теплоемкости того же газа, соответственно, при постоянном давлении и объеме.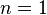 , так как
, так как  , значит, по закону Бойля — Мариотта
, значит, по закону Бойля — Мариотта  , и уравнение политропы вынуждено выглядеть так:
, и уравнение политропы вынуждено выглядеть так: 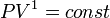 .
. , так как
, так как  , и уравнение политропы вынуждено выглядеть так:
, и уравнение политропы вынуждено выглядеть так:  .
.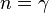 (здесь
(здесь  — показатель адиабаты), это следует из уравнения Пуассона.
— показатель адиабаты), это следует из уравнения Пуассона. , так как
, так как  , и в процессе
, и в процессе 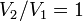 , а из уравнения политропы следует, что
, а из уравнения политропы следует, что  , то есть, что
, то есть, что 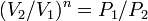 , то есть
, то есть  , а это возможно, только если
, а это возможно, только если  является бесконечным
является бесконечным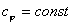

 пропорционально вызываемому тем самым повышению темп-ры
пропорционально вызываемому тем самым повышению темп-ры 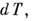 следовательно,
следовательно,  где С - теплоёмкость при П. п. Для идеального газа внутр. энергия U пропорциональна темп-ре
где С - теплоёмкость при П. п. Для идеального газа внутр. энергия U пропорциональна темп-ре  , так что. согласно первому началу термодинамики, С =
, так что. согласно первому началу термодинамики, С =  где P - давление, V - объём,
где P - давление, V - объём,  - теплоёмкость при пост. объёме. Интегрируя полученное ур-ние с учётом ур-ния состояния, находим ур-ние для политропы идеального газа:
- теплоёмкость при пост. объёме. Интегрируя полученное ур-ние с учётом ур-ния состояния, находим ур-ние для политропы идеального газа: 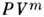 = const или
= const или  = const, где
= const, где  - теплоёмкость при пост. давлении.
- теплоёмкость при пост. давлении.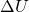 — Изменение внутренней энергии
— Изменение внутренней энергии — Количество теплоты
— Количество теплоты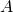 — Работа внешних сил
— Работа внешних сил — Работа совершаемая системой
— Работа совершаемая системой — Объем газа
— Объем газа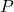 -Давление газа
-Давление газа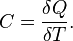
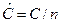 , Дж/мольК;
, Дж/мольК;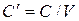 , Дж/м3К.
, Дж/м3К.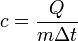 ,
, — удельная теплоёмкость,
— удельная теплоёмкость, — количество теплоты, полученное веществом при нагреве (или выделившееся при охлаждении),
— количество теплоты, полученное веществом при нагреве (или выделившееся при охлаждении),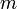 — масса нагреваемого (охлаждающегося) вещества,
— масса нагреваемого (охлаждающегося) вещества,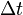 — разность конечной и начальной температур вещества.
— разность конечной и начальной температур вещества. ,
,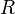 — универсальная газовая постоянная,
— универсальная газовая постоянная,  — молярная теплоёмкость при постоянном давлении,
— молярная теплоёмкость при постоянном давлении,  — молярная теплоёмкость при постоянном объёме.
— молярная теплоёмкость при постоянном объёме. ,
,
 .
.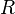 — механический эквивалент теплоты.
— механический эквивалент теплоты.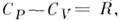 где R -газовая постоянная.Впервые было получено Ю. P. Майером (J. R. Mayer) в 1842 и ещё до работ Дж. П. Джоуля (J. P. Joule) использовано им для количеств, определениямеханического эквивалента теплоты. Для произвольной массы т (кг) вещества в состоянииидеального газа M. у. записывается в виде:
где R -газовая постоянная.Впервые было получено Ю. P. Майером (J. R. Mayer) в 1842 и ещё до работ Дж. П. Джоуля (J. P. Joule) использовано им для количеств, определениямеханического эквивалента теплоты. Для произвольной массы т (кг) вещества в состоянииидеального газа M. у. записывается в виде:  , где
, где  - молекулярная масса газа. M. у. можно получить из общего соотношения
- молекулярная масса газа. M. у. можно получить из общего соотношения  (см. Термодинамика),если учесть, что для идеального газа справедливо Клапейрона уравнение.
(см. Термодинамика),если учесть, что для идеального газа справедливо Клапейрона уравнение. ,
, — давление,
— давление,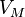 — молярный объём,
— молярный объём,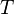 — абсолютная температура, К.
— абсолютная температура, К.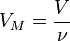 , где
, где  — количество вещества, а
— количество вещества, а 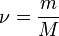 , где
, где  — масса,
— масса, 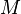 — молярная масса, уравнение состояния можно записать:
— молярная масса, уравнение состояния можно записать: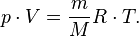
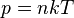 где
где  - концентрация атомов,
- концентрация атомов,  - постоянная Больцмана.
- постоянная Больцмана. , значение которой необходимо было измерять для каждого газа:
, значение которой необходимо было измерять для каждого газа: