Пропорциональное звено.
Уравнение звена Передаточная функция Переходная функция Импульсная переходная функция представляет мгновенный бесконечно большой амплитудой импульс.
Площадь мгновенного импульса равняется коэффициенту передачи звено. Частотные характеристики КПФ звена W(jω)=к. АФЧХ звена в комплексной плоскости представляет точку на вещественной оси, удаленную от начало координат на расстояние к. Модуль КПФ А(ω)=к, т.е. амплитуда выходного колебания не зависят от частоты. Аргумент КПФ φ(ω)=0, т.е. выходные колебания совпадает по фазе с колебаниями на входе на всех частотах (сдвиг фаз отсутствует). Выражение ЛАЧХ звена имеет вид ЛАЧХ звена представляет прямую, параллельную оси частот (рис. 6.1) ЛФЧХ звена представляет прямую, совпадающей с положительной вещественной осью (φ(ω)=0).
Рисунок 9.1. ЛАЧХ и ЛФЧХ пропорционального звена 3. П – регулятор. П – регулятором называется такой регулятор, у которого перемещение РО пропорционально отклонению регулируемой величины от заданного значения.
где Передаточная функция П – регулятора
т.е. П – регулятор представляет пропорциональное звено. Основным преимуществом П – регулятора является высокая скорость регулирования (пропорционально скорости изменения регулируемой величины). Главный недостаток – наличие остаточного отклонения регулируемой величины (статическая ошибка).
|

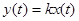 , где x(t) – входная, y(t) – выходная величины, к – передаточный коэффициент.
, где x(t) – входная, y(t) – выходная величины, к – передаточный коэффициент.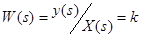
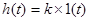 , т.е. при подаче на вход звена единичного скачка, выходная величина копирует изменение входной величины без запаздывания и искажения, но в другом масштабе. Поэтому пропорциональное звено называют еще безинерционным.
, т.е. при подаче на вход звена единичного скачка, выходная величина копирует изменение входной величины без запаздывания и искажения, но в другом масштабе. Поэтому пропорциональное звено называют еще безинерционным.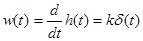
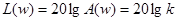

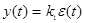 (12.1)
(12.1)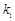 параметры настройки П –регулятора.
параметры настройки П –регулятора.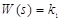 (12.2)
(12.2)


