Частотные характеристики автоматических систем.
На основе частотных характеристик разработаны инженерные частотные методы исследования САУ. Частотные характеристики позволяют просто выявлять влияние того или иного параметра на динамические свойства системы. Кроме того, частотные характеристики можно определить экспериментально. Частотные характеристики описывают вынужденные колебания на выходе системы, вызванные гармоническим воздействием на входе. Эти характеристики строятся на основании их комплексных передаточных функции (КПФ). КПФ системы (звена) W(j Комплексные изображения входного и выходного сигнала имеют вид
Отсюда можно определить КПФ системы W (j где A ( КПФ можно представить и в алгебраической форме W (j где P( A ( A ( КПФ на комплексной плоскости определяется вектором, длиной равной модулю КПФ, а поворот вектора определяется аргументом КПФ (рис 6.1) кривую, которую описывает конец вектора КПФ, при изменении частоты от нуля до бесконечности называет амплитудной фазовой частотной характеристикой (АФЧХ).
Рисунок 6.1 АФХЧ Зависимость модуля КПФ от частоты амплитудной частотной характеристикой (АЧХ). Зависимость аргумента КПФ от частоты называет фаза – частотный характеристикой (ФЧХ). Зависимость модуля КПФ от частоты амплитудной частотной характеристикой (АЧХ). Физический смысл A ( Построение АФЧХ сложных систем сопровождается большой затратой времени, поскольку при построении АФЧХ системы необходимо перемножать АФЧХ отдельных ее элементов. Исследование системы упрощается, если пользоваться логарифмическим частотным характеристикам (ЛЧХ). В этом случае ЛЧХ системы получается сложением ЛЧХ отдельных ее элементов, т.е. операция умножения заменяется операциями сложения. Если прологарифмировать КПФ, получим
ln W (j
Таким образом, ЛЧХ системы представляет собой совокупность двух характеристик ln A ( Зависимость логарифма модуля ln A ( Обычно на ось ординат принято откладывать не ln A ( Зависимость аргумента КПФ φ(ω) от частоты, отложенной по оси абсцисс в логарифмическом масштабе, называется логарифмической фазовой частотной характеристикой (ЛФЧХ). Примеры построения ЛАЧХ и ЛФЧХ показаны на рис 4.2.
Рисунок 6.2 ЛАЧХ и ЛФЧХ
Для удобства пользования логарифмическим масштабом на ось абсцисс обычно наносят значения самих частот, логарифмы которых отложены по этой оси.
|

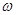 ) представляет собой отношение изображении в виде комплексных чисел выходной и входной величин системы (звена) в установившемся режиме гармонических колебаний, т.е. W(j
) представляет собой отношение изображении в виде комплексных чисел выходной и входной величин системы (звена) в установившемся режиме гармонических колебаний, т.е. W(j 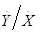 , где
, где 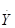 и
и  комплексы выходной и входной величин, определяется следующим образом. Если на вход системы подать синусоидальный сигнал x = Ax sin(
комплексы выходной и входной величин, определяется следующим образом. Если на вход системы подать синусоидальный сигнал x = Ax sin(  = Ax e j(ωt + φ
= Ax e j(ωt + φ  );
);  = Ay e j(ωt + φ
= Ay e j(ωt + φ  )
)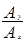 . e j(φ
. e j(φ  - φ
- φ 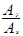 – модуль КПФ, φ(ω) = φy – φx – аргумент КПФ.
– модуль КПФ, φ(ω) = φy – φx – аргумент КПФ. и φ(ω) = arctg
и φ(ω) = arctg 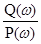 (6.3)
(6.3)




