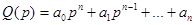Преобразование Лапласа.

При исследовании и расчетах АС часто обращаются к математическому методу, который получил название преобразование Лапласа. Этот метод позволяет функцию х(t) одного переменного (обычно времени t) преобразовать в функцию х(р) другого переменного (как правило, р) посредством соотношения:

,

где р=а+jb – произвольная комплексная величина,

а и b – вещественные переменные,

х(t) – оригинал,

х(р) – изображение.

 

Сокращенно преобразование Лапласа записывается так:

х(р) = L[ х(t)]

Преобразование Лапласа дает возможность выполнить алгебраизацию дифференциальных уравнений, т.е. операции дифференцирования и интегрирования заменить алгебраическими операциями умножения и деления. При этом первая производная от х будет иметь изображение рх(р) и т.д., т.е. производная от х n -го порядка будет выражаться как произведение оператора р в n -ой степени на изображение х(р):

Интеграл заменяют дробью в числите которой изображение, а в знаменателе – оператор р:

Отношение изображения по Лапласу выходной величины к входной величине при нулевых начальных условиях называется передаточной функцией звена (элемента) автоматической системы управления.

Допустим уравнение звена, преобразованное по Лапласу при нулевых начальных условиях, имеет вид:

Х_вых(р)(a₀pⁿ+a₁p^n-1+ …+aⁿ)=x_вх(p)(b₀p^m+b₁p^m-1+ …+b_m),

Откуда:

Величину:

,

называют передаточной функцией звена. K(p) и Q(p) – полиномы комплексного переменного р:

Понятие передаточной функции существенно упрощает решение инженерных задач при расчетах и наладке автоматических систем управления. Так, зная передаточную функцию системы, с учетом Х_вых(р) по обратному преобразованию Лапласа, можно найти переходный процесс системы.

Переходная функция, или переходная характеристика, h(t) представляет собой переходный процесс на выходе звена или системы, возникающий при подаче на его вход скачкообразного воздействия при величине скачка, равной единице (при нулевых начальных значениях). Такое входное воздействие называется единичной ступенчатой функцией и обозначается x₁(t)=1(t), что соответствует х₁=0 при t£ 0 и х₁=1 при t> 0. Предполагается, что единица имеет ту же размерность, что и физическая величина на входе звена или системы.

Если входное воздействие представляет собой не единичную ступенчатую функцию x₁=N1(t), то выходная величина будет равна x₂=Nh(t).

Таким образом, более строго переходную функцию можно определить как отношение выходной величины звена х₂(t) к высоте ступенчатого скачка x₁=N1(t) на его вход, т.е. h(t)=N^-1x₂(t) при этом размерность h(t) соответствует размерности передаточной функции звена.
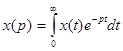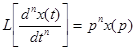
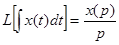
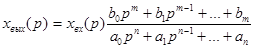
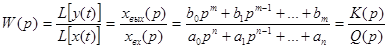