Запаздывающее звено.
Уравнение звена y(t)=x(t)(t-τ); где τ – время чистого запаздывания. Запаздывающее звено передает сигнал без искажения, но с задержкой на время τ. Передаточная функция W(s)= е – S Переходная функция h(t)=1(t-τ), т.е. переходная характеристика представляет собой повторение входного сигнала (единичного скачка), но с задержкой на время τ. Импульсная переходная функция ω(t)=δ(t-τ). Частотные характеристики КПФ звена АФЧХ звена представляет собой окружность с центром в начале координат и радиусом равным единице. Модуль КПФ Аргумент КПФ φ(ω)=-ω*τ, т.е. с увеличением частоты и времени чистого запаздывание отставание выходного колебания по фазе увеличивается.
Рисунок 11.6 АФЧХ звена.
Выражение ЛАЧХ звена L(ω)=0, т.е. эффект усиление отсутствует. ЛАЧХ звена совпадает с вещественной осью (Рис. 7.7 а) ЛФЧХ звена по абсолютной величине монотонно возрастает, с увеличением частоты и времени τ отставание по фазе возрастает (Рис. 7.7 б). А) Рисунок 11.7 а) – ЛАЧХ звена, б) – ЛФЧХ звена.
|


 .
.

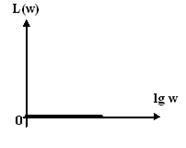 б)
б) 



