Критерий устойчивости Михайлова.
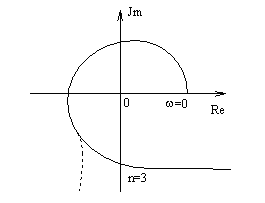
применяется для замкнутых систем. Поэтому надо “мысленно” замкнуть систему единичной ООС, найти Wз(s) и записать характеристическое уравнение замкнутой системы. Затем необходимо получить аналитическое выражение годографа Михайлова, который обозначается как D(jw). Для этого в характеристическое уравнение замкнутой системы надо подставить s=jw, разбить D(ja) на вещественную и мнимую части и построить кривую в координатах Jm-Re по контрольным точкам, т.е. D(jw)= Re D(jw)+ Jm D(jw). Формулировка критерия устойчивости Михайлова: для того, чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы годограф Михайлова начинался на вещественной положительной оси, последовательно проходил n-квадратов и уходил в бесконечность в n-том квадрате, где n- порядок системы. Принято различать три типа нахождения системы на границе устойчивости:
1) апериодическая 2) колебательная
3) бесконечный корень
Рис.7.1 2. ПИД – регулятор. ПИД – регуляторам называется регулятор, у которого перемещение РО пропорционально отклонению регулируемой величины от задания, интегралу от этого отклонения и скорости его изменения, т.е.
где Передаточная функция ПИД – регулятора
Как видно из уравнения (13.7), регулирующее воздействие состоит из пропорциональной, интегральной и дифференциальной составляющих. Последняя из них тем больше, чем больше скорость изменения отклонения регулируемой величины, т.е. регулирующее воздействие вырабатывается как бы заранее, не дожидаясь наступления значительного отклонение регулируемой величины. Введение дифференциальной составляющей закон регулирования позволяет улучшить качество переходного процесса в АСР. Однако, настройка ПИД – регулятора, связанная с определением трёх параметров, сложна, при неправильной настройке качество регулирования может оказаться хуже, чем при использовании более простых регуляторов.
|


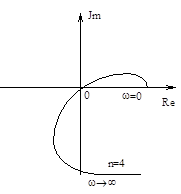
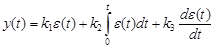 (13.7)
(13.7)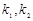 = 1/Тии
= 1/Тии 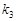 = Тд – параметры настройки ПИД–регулятора, Тд-время дифференцирования
= Тд – параметры настройки ПИД–регулятора, Тд-время дифференцирования (13.8)
(13.8)


