Идеальное дифференцирующее звено.Уравнение звена Передаточная функция W(S)=КS Переходная функция h(t)=Кδ(t), где δ(t) – дельта функция.
Частотные характеристики КПФ звена W(jω)=jкω, т.е. АФЧХ звена совпадает с положительной мнимой осью. При ω=0 А(ω)=0, с увеличением частоты А(ω) увеличивается и при ω=∞ А(ω)=∞. Модуль КПФ А(ω)=ωК, аргумент КПФ φ(ω)=90°, т.е. с увеличением частоты амплитуда выходного сигнала увеличивается. Аргумент не зависит от частоты и равен 90°, т.е. идеальное дифференцирующее звено вносит опережение, равное 90°, на всех частотах.
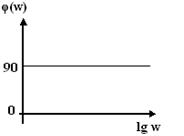
Рисунок 11.4 АФЧХ звена Выражение для ЛАЧХ звена записывается в виде ЛФЧХ идеально дифференцирующего звена – прямая, параллельная оси абсцисс, проведенная на уровне 90° а) Рисунок 11.5 а) – ЛАЧХ звена, б) – ЛФЧХ звена
|
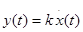, т.е. выходной сигнал пропорционально скоростью изменение входного сигнала.
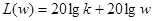. ЛАЧХ идеально дифференцирующего звена представляет собой прямую с наклоном 20 дб/дек, имеющую при ω=1 ординату, равную 20 lg к.
б) 
