Устойчивость линейных систем.
Система всегда подвергается действию внешних возмущающих сил. Эти сил в некоторых случаях стремится вывести систему из состояние равновесия. Если равновесия с определенной точностью возвращается в состояния равновесия. Если система неустойчива, она не возвращается в состояние равновесия, а удаляется от него. Обычно под устойчивостью линейной системы понимают свойства затухания переходного процесса с течением времени. Исследование устойчивости системы неразрывна связано с исследованием свободных движении системы, которые описывают однородным дифференциальными уравнениями с ненулевым начальными условиями.
Где В общем виде решение такого уравнения записывается в виде
Где Где
Для того, чтобы система была устойчивой, решение (8.2) должна удовлетворять условию
т.е. свободное движение системы Случай1. Все корни уравнение (8.3) вещественные и отрицательные ( Случай 2. Уравнение (8.3) имеет хотя бы один нулевой корень, а остальные корни вещественные (разные) и отрицательные. Тогда решение уравнение имеет вид
В этом случае система будет находится на границе устойчивости, т.к нулевой корень дает постоянную составляющую, не стремящейся с течением времени к нулю. Случай 3. Уравнение (8.3) имеет одну пару чисто мнимых сопряженных корней Тогда Составляющая от мнимых корней дает незатухающие гармоническое колебания с постоянной амплитудой Случай 4. Характеристическое уравнение имеют комплексные сопряженные корни
Если Если Случай 5. Уравнение (8.3) имеет
Если кратные корни отрицательные, то переходной процесс затухающий и система будет устойчивой. Таким образом условие устойчивости линейной системы выражается в том, что все корни характеристического уравнение должны располагаться в левой полуплоскости комплексной плоскости. Корни расположенные в правой полуплоскости делает систему неустойчивой. Мнимая ось
Рисунок 8.1. Расположения корней характеристического уравнения в комплексной плоскости Все эти выводы справедливы только для линейных систем. На практике как правило линейной моделью. В этом случае возникает вопрос, насколько заключение об устойчивости системы, сделанное по линеаризованным уравнениям, будет справедливо для реальных систем. На этот вопрос дан ответ в теоремах Ляпунова об устойчивости. Теорема 1. Если характеристическое уравнение линеаризованной системы имеет все корни с отрицательными вещественными частями, то действительная система будет устойчива. При этом никакие, отброшенные при линеаризации уравнения члены второй и высших степеней отклонения регулируемого параметра не могут изменить устойчивость системы. Теорема 2. Если характеристическое уравнение линеаризованной системы имеет хотя бы один корень с положительной вещественной частью, то действительная система будет неустойчива. При этом никакие, отброшенные при линеаризации, члены второй и высших степеней отклонения регулируемого параметра не могут придать системе устойчивость. Теорема 3. При наличии нулевых и чисто мнимых корней характеристического уравнение линеаризованной системы и отсутствии корней с положительной вещественной частью значения членов второго и высшего порядка могут имеет определяющее значение при оценке устойчивости системы. Поэтому устойчивость исходной системы нужно оценивать по исходным же уравнениям.
|

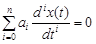 (8.1)
(8.1) – постоянные коэффициенты.
– постоянные коэффициенты. (8.2)
(8.2) – постоянные, определяется начальными условиями,
– постоянные, определяется начальными условиями,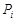 – корни характеристического уравнение
– корни характеристического уравнение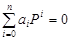 (8.3)
(8.3)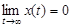 (9.4)
(9.4) при
при  должен стремится к нулю при произвольных постоянных интегрирование. Условие (8.4) является аналитическим выражением устойчивости системы и выполняется в том случае, когда все корни характеристического уравнение (8.3) имеют отрицательные вещественные части.
должен стремится к нулю при произвольных постоянных интегрирование. Условие (8.4) является аналитическим выражением устойчивости системы и выполняется в том случае, когда все корни характеристического уравнение (8.3) имеют отрицательные вещественные части.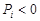 ),
),  . В этом случае переходной процесс с течением времени апериодически будет стремится к нулю.
. В этом случае переходной процесс с течением времени апериодически будет стремится к нулю.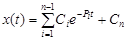
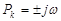 , а остальные вещественные (разные) и отрицательные.
, а остальные вещественные (разные) и отрицательные.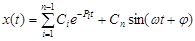
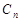 . Система в этом случае будет неустойчивой (на границе устойчивости).
. Система в этом случае будет неустойчивой (на границе устойчивости).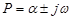 , остальные вещественные (разные) и отрицательные. В этом случае составляющие с переменной амплитудой
, остальные вещественные (разные) и отрицательные. В этом случае составляющие с переменной амплитудой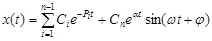
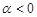 , то возникшее колебательные движение будет затухающим и система будет устойчиво.
, то возникшее колебательные движение будет затухающим и система будет устойчиво.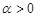 , то колебание незатухающие и система неустойчива.
, то колебание незатухающие и система неустойчива. – кратных корней, а остальные корни вещественные (разные) и отрицательные, тогда
– кратных корней, а остальные корни вещественные (разные) и отрицательные, тогда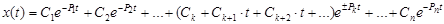
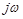 плоскости корней служит границей устойчивости.
плоскости корней служит границей устойчивости.



