Методом простых итераций
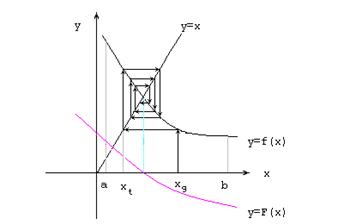
Пусть корень уравнения находится на отрезке [a,b] (рис.4.3). Для использования метода итераций исходное уравнение F(x) = 0 нужно привести к виду x = f(x). Если известно начальное приближение к корню x = x1, то подставив его в правую часть уравнения x = f(x), получим новое приближение x2 = f(x1). Затем аналогичным образом получим Итерационный процесс сходится к корню уравнения, если |fў(x)|<1 на отрезке, содержащем корень уравнения. Если выполняется неравенство –1<f ΄(x)<0, то корень уравнения всегда находится на отрезке [xk, xk+1] или [xk+1,xk] и условие окончания итерационного процесса имеет вид неравенства [xk+1 – xk]<e.
Рис.4.3. Метод простых итераций Переход от уравнения F(x) = 0 к уравнению f(x) можно осуществить следующим образом. Умножим левую и правую части уравнения F(x) = 0 на некоторую константу h и добавим к обеим частям уравнения неизвестное x. Эти действия не изменяют корней уравнения: hF(x) + x = 0*h + x; hF(x) + x = x. Обозначив f(x) = hF(x) + x, перейдем к уравнению x = f(x). Величину h необходимо выбрать такой, чтобы выполнялись неравенства |f '(x)|<1, f '(x)<0 на отрезке, содержащем корень уравнения. Исходными данными для программы, соответствующей приведенному алгоритму, являются грубое значение корня и точность вычисления. Условием выхода из итерационного процесса служит неравенство |xg –x t|<e, при этом искомым значением является xt Пример 4.3. Решение уравнения Преобразуем уравнение к виду #include <iostream> #include <conio.h> #include <math.h> using namespace std;
int main() { float xt, xg = 2.3, eps = 0.001, x = 5*eps; int step = 0; while (fabs(x)>=eps) { xt = -0.2*(xg*xg*xg – 2*xg*xg –3)+xg; x = xt-xg; step++; xg = xt; } cout << "Корень = " << xt << " и получен на шаге " << step; getch(); return 0; } Решение уравнения f(x) = 0 с заданной точностью e
|

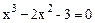 методом итераций.
методом итераций.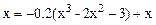 .
.


