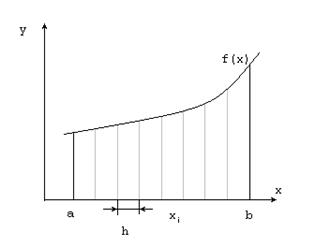
Вычисление по формуле Симпсона путем деления отрезка [a,b] на множество более мелких отрезковДля нахождения интеграла вычислим площадь под графиком функции, являющейся подынтегральным выражением(рис.4.2). Здесь a и b - пределы интегрирования; xi = a + i(b - a)/n. Для использования формулы Симпсона разбиваем отрезок [a,b] на n (четное) более мелких отрезков. Формула Симпсона имеет вид: Здесь n - четное число делений интервала интегрирования; xi = a + i(b – a)/n. Алгоритм состоит в циклическом выполнении расчетов f(xi). При этом следует отдельно рассмотреть случаи для границ интегрирования f(a) и f(b) и учесть, что при нечетном номере вычисляемого элемента значение функции умножается на 4, при четном - на 2. При конечных значениях отрезка умножение не производится.
Рис.4.2. Вычисление интеграла по формуле Симпсона. Пример 4.2. Вычисление интеграла #include <iostream> #include <conio.h> #include <math.h> using namespace std;
int main() {unsigned long i, n; float a,b,x,h,y,s; cout << "Четное количество делений -> "; cin >> n; a = 0; b = 1.8; s = 0; x = a; h = (b – a)/n; for (i = 0; i <= n; i++) { y = (1/(1+sqrt(x)); x = x + h; if (i % 2!= 0) s = s + 4*y; else if (i == 0 || i == n) s = s + y; else s = s + 2*y; } s*=h/3; cout << "S = " << s; } Вычисление с заданной точностью e корня уравнения F(x)=0
|
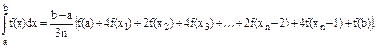
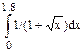по формуле Симпсона.
