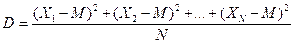Дисперсия.

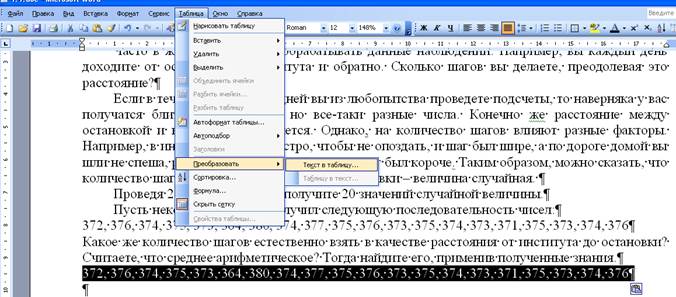
Лабораторная работа № 6

Математическая статистика

Дисперсия.

Часто в жизни приходится обрабатывать данные наблюдений. Например, вы каждый день доходите от остановки до института и обратно. Сколько шагов вы делаете, преодолевая это расстояние?

Если в течение нескольких дней вы из любопытства проведете подсчеты, то наверняка у вас получатся близкие друг другу, но все-таки разные числа. Конечно же расстояние между остановкой и корпусом не меняется. Однако, на количество шагов влияют разные факторы. Например, в институт вы шли быстро, чтобы не опоздать, и шаг был шире, а по дороге домой вы шли не спеша, разговаривая с подругой, - ваш шаг был короче. Таким образом, можно сказать, что количество шагов от корпуса института до остановки – величина случайная.

Проведя 20 наблюдений, вы получите 20 значений случайной величины.

Пусть некоторый студент получил следующую последовательность чисел:

372, 376, 374, 375, 373, 364, 380, 374, 377, 375, 376, 373, 375, 374, 373, 371, 375, 373, 374, 376

Какое же количество шагов естественно взять в качестве расстояния от института до остановки? Считаете, что среднее арифметическое? Тогда найдите его, применив полученные знания.

 

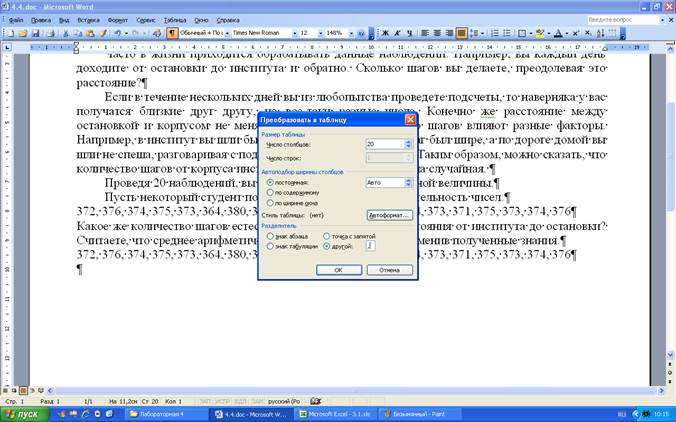
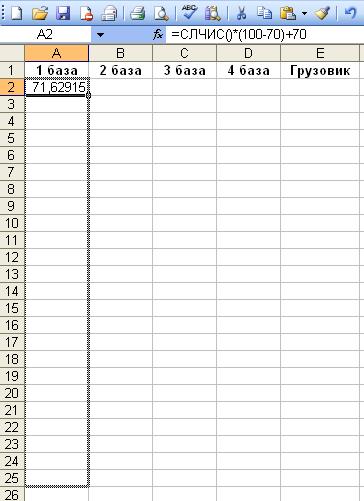
Для начала полученный ряд чисел удобнее преобразовать в линейную таблицу.

 

 

После наведения красоты получаем следующую табличку. Ее уже можно скопировать в Excel

Находим среднее арифметическое этого ряда чисел

 

Конечно тот факт, что мы провели 20 наблюдений и нашли среднее арифметическое гораздо больше приближает нас к истинному расстоянию между остановкой и институтом, однако, все-таки хотелось бы знать насколько же мы близки к истине.

Для этого математики ввели специальную величину и назвали ее дисперсией (т.е. разброс данных).

 

Определение 1. Дисперсия – это среднее арифметическое квадратов разностей между значениями случайной величины и ее средним значением.

 

Обозначим значения случайной величины за Х₁, Х₂, Х₃, … Х_N, а среднее арифметическое буквой М. Тогда

Из формулы вам должно быть видно, что чем меньше дисперсия, тем меньше отклоняются результаты наблюдений от своего среднего значения и тем ближе среднее значение к истинному. В частности, если дисперсия равна нулю, то все значения случайной величины совпадают со своим средним значением и между собой.

 

Задание 1. Подумайте, зачем разности между значениями случайной величины и ее средним значением нужно возводить в квадрат?

 

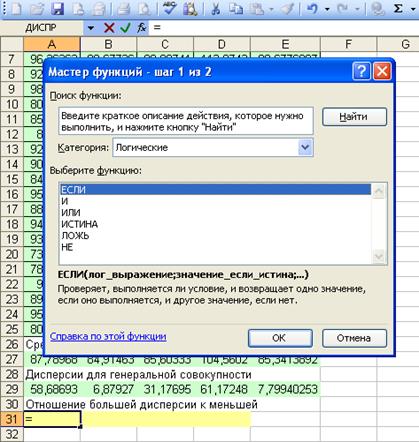
Задание 2. Найдем дисперсию для наблюдений нашего студента.

Уверена, что для вас это задание и без подсказок не составит никакого труда!

Ответ: дисперсия для выборки (ДИСП) = 9,368421, дисперсия для генеральной совокупности (ДИСПР) = 8,9.

 

Пусть наш студент сагитировал несколько своих друзей провести тот же самый эксперимент. Через несколько дней они представили по 20 результатов наблюдений каждый. Сам студент тоже участвовал в этом эксперименте, т.е. считал шаги снова.

 

Можно ли по получившимся рядам значений узнать, какие из результатов принадлежат нашему студенту?

 

Для решения этой задачи математики советуют сравнить дисперсии и средние значения.

 

Они утверждают, что дисперсия и среднее значение так же индивидуальны, как отпечатки пальцев.

Если наблюдения проводил один и тот же человек, то дисперсии и средние значения во всех наблюдениях будут близки, а если разные люди, то далеки.

 

Если число наблюдений лежит в промежутке от 25 до 50, то

1) дисперсии можно считать далекими, если отношение большей дисперсии к меньшей больше 2;

2) средние значения можно считать далекими, если модуль разности средних, деленный на квадратный корень из суммы дисперсий больше 0,6.

Если и дисперсии, и средние значения являются близкими, то можно сделать вывод, что наблюдения наверняка проводились одним и тем же человеком.

 

Метод сравнения средних значений и дисперсий используется в самых разных отраслях человеческой деятельности. В медицине – для установления диагноза, в литературоведении – для определения автора произведения, в криминалистике – для розыска преступников.

 

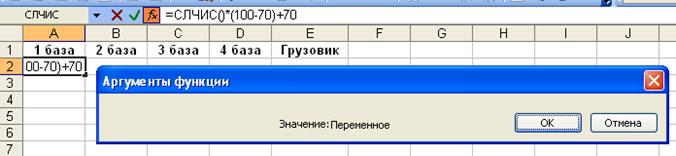
Задание 3. Органами милиции задержан грузовик с помидорами, похищенными с овощной базы. В городе всего четыре таких базы, каждая из которых получает помидоры из своего сельскохозяйственного района. Определите, с какой базы были вывезены помидоры. Расследование осложняется тем, что на всех базах есть помидоры именно такого сорта.

Исходные данные для решения нашей задачи следующие.

Пусть вес помидора на соответствующих базах и в грузовике изменяется в пределах (что зависит от плодородности почвы в различных районах, от количества вносимых удобрений, погодных условий и т.д.):

1 база (70; 100)

2 база (80; 90)

3 база (75; 95)

4 база (90; 120)

Грузовик (80; 90)

 

Для решения этой задачи, естественно, воспользуемся методом сравнения средних значений и дисперсий.

 

Алгоритм действий:

1. Заносим в таблицу Excel исходные данные следующим образом: для каждой базы и грузовика заносим формулу для генерации компьютером случайного числа и протягиваем на 25-50 наблюдений на ваше усмотрение.

 

 

 

1. Находим для каждой базы и грузовика среднее значение и дисперсию. Формулу задаем для базы 1, на базы 2 – 4 и грузовик протягиваем вправо.
2. Находим отношение большей дисперсии к меньшей для грузовика и каждой из баз (сравниваем каждый раз грузовик с каждой из баз по очереди). Формулу задаем для базы 1, на базы 2 – 4 и грузовик протягиваем вправо.

 

1. Находим отношения модуля разности средних к квадратному корню из суммы дисперсий для грузовика и каждой из баз

 

 

Продолжить формулу самим (знаменатель)

1. Определить близость дисперсий каждой базы и грузовика, используя логическую функцию «ЕСЛИ».
2. Определить близость средних каждой базы и грузовика, используя логическую функцию «ЕСЛИ».
3. Находим ту базу, для которой «близки» с грузовиком одновременно и дисперсии и средние значения. Снова используем функцию «ЕСЛИ» и «И».

Проанализировать ответ.