Текущий ежегодный спрос на товар можно выражать в относительном измерении в долях от конечного суммарного потребления.
Данная величина в моделях обозначается f и называется текущим относительным потреблением. Она имеет следующую взаимосвязь с вышеназванными величинами: n = f * m. (1) К началу каждого года можно определить долю конечной потребности в товаре, которая уже является удовлетворенной. Данная величина называется накопленным относительным потреблением и обозначается F. Для каждого года t данная величина путем суммирования текущего относительного потребления fi предыдущих лет:
Для первого года ЖЦТ величина F принимается равной нулю, так как удовлетворения спроса данным товаром еще не было. Данная величина является важнейшей переменной в моделях диффузии инновации. На начальном этапе, когда инновация как способ удовлетворения потребности появляется на рынке, в обществе практически нет информации о ней и результатах ее применения. Она появляется в результате первых пробных покупок потребителями – новаторами. Их влияние на динамику потребления товара отражено в модели в так называемом коэффициенте инновации – p. Его экономический смысл заключается в том, что он показывает уровень потребления товара в относительном выражении в первый год ЖЦТ, когда опыта потребления данной инновации еще нет. Область значений коэффициента инновации: p ∈ [0, 1]. Получив положительный опыт удовлетворения потребности, новаторы передают его другим покупателям, т.н. имитаторам, которые, в свою очередь, также осознав потребность и удовлетворив ее с помощью покупки, распространяют информацию об инновации далее. Влияние данного процесса показывается в моделях диффузии с использованием коэффициента имитации - q, который показывает отношение текущего потребления покупателей – имитаторов к уже накопленному объему потребления данной инновации (F). Область определения коэффициента: q ∈ [0, 1]. Таким образом, с распространением информации происходит осознание потребности все большими массами потенциальных потребителей инновации, что ведет к расширению спроса на нее на этапе роста кривой жизненного цикла.
На этапе спада рост потребления ограничивается увеличением количества потребителей, окончательно удовлетворивших потребности, то есть явлением исчерпания потребности рынка (m), в результате чего тенденция роста объемов заменяется тенденцией спада. Математическое моделирование данных процессов строится на следующем принципе модели ВASS). Как видно в табл. 1, в модели диффузии текущее потребление определяется произведением двух сомножителей: f = (p + qF)(1 - F). Первый сомножитель: (p + qF) – моделирует рост объемов потребления товара с накоплением удовлетворенной потребности и, как следствие, использование информации о товаре. Второй сомножитель: (1 - F) – моделирует исчерпание емкости рынка в процессе удовлетворения конечной потребности. На этапе роста ЖЦТ увеличение первого сомножителя доминирует над снижением второго. К началу спада данное соотношение меняется в обратную сторону. Аналогичную структуру имеют и другие модели диффузии, поэтому принципы моделирования цикла распространения инновации для них будут аналогичными вышеназванным.
На практике жизненный цикл спроса товара будет включать в себя жизненные циклы всех способов удовлетворения исходной потребности. Этот факт имеет ряд чрезвычайно важных последствий и в первую в связи с конкуренции на рынке. Например, при рассмотрении жизненных циклов конкретных товаров или технологий может происходить сложное конкурентное взаимодействие, которое будет заключаться в перераспределении объемов сбыта, направленных на удовлетворение рыночной потребности, между различными продуктами и фирмами. Данное явление называется конкурентным замещением, и без его рассмотрения описание процессов, лежащих в основе изменения рыночных позиций товаров во времени, будет неполным.
Рисунок 1 Графическая модель полного замещения.
Под замещением мы будем понимать переход части спроса от одного способа удовлетворения потребности к другому. В том случае, если суммарный объем удовлетворения рыночной потребности с помощью всех конкурирующих технологий в каждый период времени остается равным величине, определяемой значением кривой жизненного цикла спроса для данного периода, следует вести речь о полном замещении. В этом случае, часть рынка, принадлежащего менее эффективной технологии, полностью переходит к заменителю. [9, с. 57]
S = S T
Модели бинарного (двухкомпонентного) замещения являются, как правило, производными от моделей диффузии, могут применяться для решения ряда практических задач прогностического характера. Они также могут эффективно применяться для построения прогнозных кривых жизненных циклов товаров на основе эталонной кривой ЖЦТ товарной группы с учетом реальной динамики сбыта товара, сложившейся в результате влияния эффекта замещения. Основные уравнения бинарного замещения на базе моделей диффузии приведены в табл. 1. Приведем базовую гипотезу и поясним смысл уравнения модели бинарного замещения.[9,c. 59] 1. Гипотеза модели бинарного замещения. Вводятся две группы величин, характеризующих динамику объемов продаж товара: f' и F' – объемы потребления, остающиеся за товаром предприятия; f'' и F'' – объемы потребления, отходящие к конкурентам (замещение товара относим ко всему внешнему рыночному конкурентному фону, без выявления, какими именно товарами и в каких объемах осуществлено замещение). Будем рассматривать только полное замещение, когда величина m остается постоянной. То есть уравнения: f = f' + f''; F = F' + F'' будут верны для любого этапа. Тогда на базе уравнений модели диффузии могут быть выведены уравнения модели бинарного замещения (их варианты для разных моделей диффузии приведены в табл. 1). 2. Уравнение модели бинарного замещения. Запись зависимости будет зависеть от исходного типа модели диффузии, которая используется. Для исследования жизненных циклов на примере компьютерных услуг рекомендуется модель Басса. Тогда уравнение расчета объема реализации услуг с учетом замещения примет следующий вид:
В данной модели все параметры, кроме р, - соответствуют исходной модели диффузии, величина F – рассчитывается для каждого года при построении эталонной кривой ЖЦТ товара по модели диффузии, как постоянная, величина F' – реально накопленный объем потребления товара. Коэффициент p – реальный коэффициент инновации, характеризующий процесс распространения изучаемого товара. Эмпирически установлено, что в реальных условиях конкуренции происходит разделение величины первоначального потребления на две составляющие: p' – уровень первоначального потребления непосредственно изучаемого товара; p'' – уровень первоначального потребления, отошедший к конкурентам. При полном замещении имеется соотношение: p = p' + p'' (4) Расчет величины p' достаточно просто осуществим: p' равен величине текущего относительного потребления товара первого года ЖЦТ. Подведем краткий итог рассмотрению экономической природы жизненного цикла товара. 1. Любой товар, технология (способ производства) товара в момент своего появления является инновацией. 2. Новый товар вызывает определенные инновационные изменения рыночной среды, связанные с осознанием потребности, на удовлетворение которой данный товар нацелен. 3. Динамика спроса на новый товар (жизненный цикл товара) будет иметь характер инновационного цикла, имеющий этапы возникновения, роста (связанного с распространением информации о новинке и осознанием потребности), стабилизации и спада, экономическими причинами которых, в свою очередь, будет распространение информации, постепенное исчерпывающее удовлетворение исходной потребности и наличием фактора замещения более эффективными инновациями. 4. Цикличность характера динамики рыночного спроса на любой товар выдвигает перед предприятием требование постоянного обновления своего ассортимента и учета характера жизненных циклов в товарной политике. На основе моделирования ЖЦТ может строиться прогноз изменений позиции продукции предприятия на рынке. [ 9,c. 63] Причинами неполного замещения, как правило, являются социально-экономические факторы, такие как снижение платежеспособности населения. В этом случае может возникать так называемый «отложенный спрос», в результате чего удовлетворение потребности отодвигается на более отдаленные периоды, либо, в конечном итоге, полного удовлетворения потребности не происходит. К неполному замещению также может вести неэффективная конкуренция на рынке в условиях высокого уровня его монополизации. Данное явление является сложным и малоизученным. В процессе оценки текущего положения и перспектив товара на основе построения прогноза динамики объемов продаж предлагается использовать следующую последовательность действий, которая предложенаСилаковым А. В.: 1. Определение параметров аппроксимации моделей диффузии на основе данных о динамике продаж ассортимента с законченным ЖЦТ. 2. Группировка полученных данных по товарным группам, определение усредненных параметров кривой жизненного цикла для каждой товарно-ассортиментной группы. 3. Моделирование на основе усредненных данных профиля ЖЦТ, характерного для каждой товарно-ассортиментной группы. 4. Моделирование эталонной кривой ЖЦТ для каждого товара с учетом его темпов обновления. 5. Построение сглаженной кривой ЖЦТ для каждого выпускаемого вида товара на основе эталонной кривой и данных о динамике реальных продаж с использованием модели замещения; ее экстраполяция в целях прогнозирования будущих продаж. 6. Анализ ЖЦТ на основе сопоставления реальной, сглаженной и эталонных кривых; использование прогноза объема потребления вида товара в планировании и оптимизации товарного портфеля. Основа первых трех этапов - определение усредненных параметров ЖЦТ по каждой товарно-ассортиментной группе предприятия, что необходимо для построения эталонной кривой ЖЦТ, учитывающей уровни конкурентоспособности ассортимента и работы предприятия, а также уровень социально-экономических условий базового периода. Следует отметить, что описываемый способ прогнозирования и анализа ЖЦТ основан на допущении о неизменности внутренней и внешней среды фирмы в плановом и базовом периодах. Задача построения и анализа кривых ЖЦТ по видам товаров, входящим в товарный портфель предприятия, может быть разделена на два основных блока. Первый – построение эталонных кривых, показывающих максимально возможный уровень продаж по этапам жизненного цикла товаров. Параметры этих кривых используются во втором блоке – при построении сглаженных кривых жизненного цикла товаров, учитывающих фактор замещения, который проявляется в реальной динамике сбыта. Сглаженную кривую можно рассматривать в качестве прогнозной динамики объемов продаж составляющих товарного портфеля.[9, c. 67] Для определения усредненных параметров кривых ЖЦТ товарных групп были взяты данные по объемам сбыта группы “услуги для VEB”. Были рассмотрены два товара из одной товарной группы, обладающих длительностью ЖЦТ от 4 лет, с помощью метода наименьших квадратов были определены параметры моделей диффузии и построены теоретические кривые. Некоторой сложностью аппроксимации моделей диффузии по эмпирическим данным является нелинейный характер их уравнений. Поэтому общепринятые статистические формулы расчета параметров моделей аппроксимации неприемлемы в данном случае. Определение параметров моделей производилось с помощью табличного процессора MS Excel в несколько этапов. На первом этапе определяется параметр m как сумма объема реализации за весь период жизненного цикла продукции по формуле.
где i – номер года. Незаконченность их ЖЦТ порождали некоторую сложность с точки зрения выявления величины m. Для решения этой проблемы, мы воспользовались гипотезой о том, что на заключительном отрезке кривой уменьшение объемов потребления продукта происходит практически равномерно и, в результате характер линии ЖЦТ на данном отрезке приближается к прямой. Тогда возможно рассчитать предварительные прогнозные значения объемов продаж на 2 – 3 года, последующие за плановым периодом, и в течение которых предполагается снятие данных. Формула прогноза выводится на основе формулы среднего темпа роста и имеет следующий вид:
Далее для каждого года определяется величина текущего относительного потребления fi на основе зависимости (1): fi = ni / m (7) Приняв накопленное относительное потребление первого года (F1) равным нулю, для последующих лет данная величина может быть рассчитана следующим образом: Fi = fi - 1 + Fi - 1, (8) где i – номер года. Определение параметров модели производится с использованием методов математического программирования. Расчеты производились автором с помощью встроенного в MS Excel пакета «Поиск решения». На основе основного уравнения метода наименьших составляется целевая функция задачи поиска параметров аппроксимации модели диффузии для описания кривой ЖЦТ. Как известно, в основе метода наименьших квадратов лежит минимизация функции квадрата разности эмпирических значений показателя и значений того же показателя, вычисленных с помощью регрессионной модели. В данном случае целевая функция выражается как квадрат разности эмпирического и теоретического значения текущего потребления товара (fi или ni). В свою очередь, теоретическое значение выражается как функция текущего относительного потребления от накопленного к началу рассматриваемого года относительного потребления, заданная через базовое уравнение модели Ф. Басса. В окончательном виде функция поиска оптимальных параметров модели выглядит следующим образом: S2 = Цель решения оптимизационной задачи – найти экстремальное значение целевой функции при действии ограничений на параметры по их области значений q ≥ 0, (10) q ≤ 1, (11) p ≥ 0, (12) p ≤ 1, (13) Решив нелинейную оптимизационную модель, описываемую целевой функцией (9) и ограничениями (10 – 13), получаем искомые параметры уравнения модели диффузии, оптимальным образом аппроксимирующие кривую жизненного цикла продукции. После определения параметров модели необходимо произвести оценку тесноты связи с использованием индекса корреляции (R) и определения его значимости по t-критерию Стьюдента, а также адекватности модели исходным данным на основе F-критерия Фишера по стандартной статистической методике. Рассмотрим методику расчета параметров модели диффузии в табличной форме на примере группы услуг «Разработка сайта». В эту группу входят услуги по разработке веб-сайтов и электронных магазинов. (Данные по расчетам предоставлены в таб. 2) В столбике приведены реальные данные по сбыту за 2007 – 2011 годы. Прогноз на 2012 – 2014 годы приведенный в этом же столбике рассчитан по формуле (6). Сумма объемов реализации есть величина m, которая приведена в данной строке в графе «Всего» в данном случае m = 499 штук Далее, по формуле (7) рассчитываются значения для строки fреал. Например, для 2007 года f = 26 шт. / 499 шт. = 0,0521 По формуле (8) определяются значения для строки Fреал. Для 2008 года F = 0 + 0,052104208 = 0,052104208; для 2009 года: F = 0,052104208+ 0,06012024 = 0,112224449 Далее, в строке fi задаются расчетные значения текущего относительного потребления, выраженные как функция от величины Fреал в соответствии с уравнением модели Басса: (проиллюстрируем на основе расчета значения ячейки столбца 2008 года, получаемого после проведения процедуры оптимизации) f2008 = (0,13+0,74*0,06010025)(1-0.06012024) = 0,0048870772. В следующей строке задается квадрат разности S2 реальных и расчетных значений величины текущего относительного потребления. После проведения процедуры оптимизации в ячейке столбца 2008 года получится расчетное значение следующим образом: S^2 = (0,06012024– 0,048870772)^2 = 0,000127 После формализации всех зависимостей в соответствующих ячейках таблицы необходимо в опции «Сервис» панели инструментов программы Excel выбрать пункт «Поиск решения». На экране высвечивается диалоговое окно. В данном окне в поле «Изменяя ячейки» необходимо задать интервал ячеек, в которых находится область вывода значений функции аппроксимации. В поле «Установить целевую» необходимо указать ссылку на ячейку вывода значения целевой функции вида (9). Она находится в таблице в строке «S2» в графе «Всего». В поле «Ограничения» необходимо задать для ячеек вывода искомых параметров модели ограничения (10) – (13). После проведения процедуры оптимизации с помощью пакета «Поиск решения» найдем p,q. Таблица 2 Данные по расчетам p,q
В результате аппроксимации были получены значения коэффициентов p=0,013 и q=0,74 для эталонной кривой. Теперь построим эталонную модель на основании найденных коэффициентов. (данные расчетов таб. 2) Для примера, на 2011 год: fэталонная = (0,013 + 0,74*0,013)*(1-0,013) = 0,0223 Сделаем прогноз для услуги “GMS”. Для оценки m возьмем среднее значение кол-ва разработок для веба и умножим на количество студий. На сайте newkaliningrad.ru зарегистрировано 41 компаний – конкурентов. По уравнению модели замещения, соответствующей модели f¢сглаженная = (p' + q F¢реальная)*(1- Fэталонная) p’= 0,0048 (т.к. по условию p' равен величине текущего относительного потребления товара первого года ЖЦТ) На примере значений столбца 2011 года: f¢сглаженная = (0,0048 + 0,74* 0,0145)*(1- 0,0353) = 0,014982 Таблица 2 Данные для построения модели замещения
Результат предоставлен на графике (рис. 6)
Рисунок 3. Эталонная, реальная, сглаженная кривые CMS Отметим, что точность прогноза по модели замещения повышается при увеличении периода основания прогноза, то есть, значения прогнозной кривой более поздних лет в значительно большей мере соответствуют значению реальной кривой, чем значения ранних периодов ЖЦТ. В том случае, когда реальный ЖЦТ товара достаточно адекватно моделируется с помощью модели замещения, следует говорить о наличии негативных симптомов. Действительно, наличие (эмпирическое подтверждение) фактора замещения при построении ЖЦТ товара говорит о том, что рыночные позиции его являются более слабыми, чем у товара-эталона. Это является следствием снижения конкурентоспособности продукции предприятия.[c.87, 99]
|

 (2)
(2)

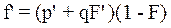 (3)
(3) (5)
(5)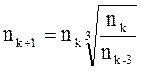 , (6)
, (6) (fi – (p + qFi )*(1 – Fi))2 → min, (9)
(fi – (p + qFi )*(1 – Fi))2 → min, (9)




