Задача 1.
Дана таблица распределения 100 заводов по производственным средствам Х (тыс. ден. ед.) и по суточной выработке Y (т). Известно, что между Х и У существует линейная корреляционная зависимость. Требуется: а) найти уравнение прямой регрессии у на х; б) построить уравнение эмпирической линии регрессии и случайные точки выборки (Х, У).
Решение: а) найдем выборочный коэффициент корреляции по формуле (2):
Для этого необходимо вычислить выборочное среднее Найдем неизвестные значения: 1.
2. Аналогично найдем
(формулы 5,11,10,9).
3. Найдем 4. По формуле (2) вычислим коэффициент корреляции:
5. Оценим значимость коэффициента корреляции по формуле (12):
т.к. 7,609>3, то б) т.к.
Оценкой теоретической линии регрессии является эмпирическая линия регрессии, уравнение которой имеет вид:
Составляем уравнение эмпирической линии регрессии
Строим линию регрессии и случайные точки
|

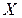
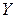
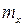
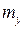
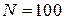

 ; выборочное среднее
; выборочное среднее 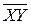 ; выборочные дисперсии
; выборочные дисперсии 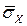 и
и  :
: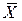 и
и 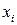
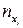
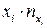
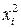
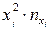
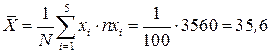
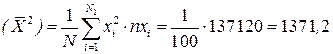

 и
и 
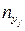


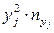
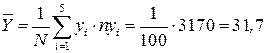 (формула 4)
(формула 4)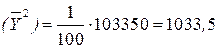 (формула 8)
(формула 8)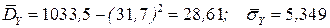 (формулы 6,7)
(формулы 6,7)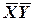 по формуле (3):
по формуле (3):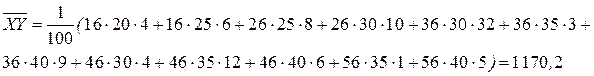
 .
.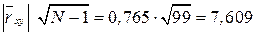
 - значимый, т.е.
- значимый, т.е.  зависит от
зависит от 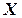 и
и 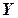
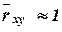 , то можно считать, что между
, то можно считать, что между 
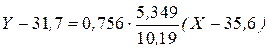
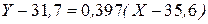 или окончательно
или окончательно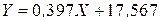
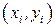 а
а


