Транспортная задача по критерию времени
В некоторых транспортных задачах вместо тарифов задают величины tij – время доставки товара от i- го поставщика к j- му потребителю (например, при перевозках скоропортящихся грузов). Требуется найти план перевозок, при котором будет затрачено минимальное время. Эта задача не является ЗЛП, поскольку целевая функция не линейна относительно переменных xij. Рассмотрим метод решения этой задачи, который называется «методом запрещенных клеток». Алгоритм решения (для закрытой модели ТЗ) содержит следующие этапы: 1) Находим опорное решение, например, методом северо-западного угла. 2) Находим время, затрачиваемое на этот план: 3) Пытаемся улучшить решение, для чего: a) Вычеркиваем свободные клетки, в которых время перевозки не меньше, чем Т1 (эти клетки нет смысла занимать) b) Для самой продолжительной среди занятых клеток строим разгрузочную цепь- замкнутую линию с прямыми углами в вершинах. Первая вершина та, для которой строится цепь. Нечетные вершины должны попасть в занятые клетки, и они помечаются знаком плюс, четные вершины могут попасть и в занятую, и в незанятую клетки, и они помечаются знаком минус. Перебрасываемая величина 4) План будет оптимальным, а время минимальным, когда для самой продолжительной из занятых клеток нельзя построить разгрузочную цепь. Пример. Решить ТЗ по критерию времени (рассмотрим таблицу с планом перевозок по методу С-З угла).
Отметим запрещенные клетки. Целевая функция имеет значение T1=max(4;2;3;3;2;3)=4=t11. Расставим разгрузочную цепь и знаки – плюсы и минусы – в вершинах. Перебрасываемая величина D= min(50;40)=40 (минимум берем по перевозкам в отрицательных вершинах). Значение этой величины вычитаем из отрицательных вершин и прибавляем к положительным вершинам цепи, получаем новый опорный план:
Новый план не уменьшил значение целевой функции, поэтому из той же клетки строим новую цепь, где перебрасываемая величина равна 10. Повторяем пересчет плана, новый план имеет вид:
Теперь целевая функция имеет значение 3, поэтому в новом плане запрещаем очередные клетки. После этого не остается ни одной свободной незапрещенной клетки, разгрузочную цепь построить нельзя, план оптимален. Задача решена.
|

 , т.е. самое продолжительное время перевозок в занятых клетках.
, т.е. самое продолжительное время перевозок в занятых клетках.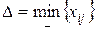 прибавляется к четным вершинам и вычитается из нечетных вершин. Для данной клетки может быть несколько цепей.
прибавляется к четным вершинам и вычитается из нечетных вершин. Для данной клетки может быть несколько цепей. bj
ai
bj
ai


 70
70




 90
90



