Векторы.

В КГ точки часто связываются направленными отрезками, см рис. 1

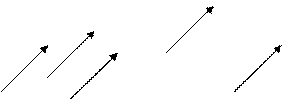
Рис.1 а) две точки, связаны направленным отрезком; б) направленные отрезки прямой

Такие отрезки прямых и есть векторы. В более общем смысле физики и инженеры используют термин вектор для обозначения любой величины, характеризуемой направлением и значением. Физические величины, такие как скорость и сила, есть векторы.

Однако вектор в этом смысле не имеет фиксированной точки приложения (позиции). Следовательно, направленные отрезки, показанные на рис. 2, являются одинаковыми векторами, поскольку имеют одно и то же направление и одинаковую длину, хотя и разные точки приложения.

 

 

Рис.2 Одинаковые векторы (идентичные свободные векторы)

Термины вектор и направленный отрезок будем использовать как синонимы.

 

Длину и направление вектора характеризуют вещественными числами. Например, вектор А имеет то же направление, что и вектор В, но В имеет длину в два раза большую, чем А, а потому можно записать В = 2А. Вектор С имеет ту же длину, что и А, но противоположное направление, а потому соотношение между ними выразится формулой С = - А.

 

А

А

Рис.3 Соотношения между векторами: (слева) выраженное с помощью вещественных чисел, (справа) через правило соединения векторов

 

Объединять векторы можно с помощью правила составления их начала одного с концом другого (head-to-tail rule), схематически представленного на рис. 3 справа. На этом рисунке конец вектора А приставлен к началу вектора В и сформирован новый вектор С, величину и направление которого определяют отрезком, соединяющим начало вектора А и конец вектора В. Этот новый вектор называют суммой векторов А и В и записывают как соотношение между ними в виде С=А+В.

Поскольку векторы не имеют фиксированной точки приложения, то для геометрического сложения векторов их можно переносить параллельно самим себе куда угодно !!!

Точки и векторы — это разные геометрические типы. Геометрическое представление точки в виде направленного отрезка [•р = (х, у,)], соединяющего некоторую опорную точку с заданной (рис. 4), следует рассматривать как сомнительное, так как опорная точка может быть где угодно, т.е. ее местоположение неопределено.

•р = (х, у,)

Рис.4

Однако существует операция, в которой связываются точки и направленный отрезок (рис. 1.) Можно использовать направленный отрезок для перемещения от одной точки к другой. Точно так же две точки определяют отрезок, проведенный между ними, а точка и вектор определяют вторую точку. Таким образом, правильная интерпретация рис. 4 состоит в том, что данный вектор можно определить как исходящий из фиксированной опорной точки (начала системы координат) и приходящий в определенную точку пространства. Важно то, что вектор, как и точка, существует независимо от опорной системы, но, дальше будет показано, что работать с их представлениями требуется в определенной системе координат.