Возможные действия с объектами каждого типа.

Рассмотрим, как можно использовать базовые типы для выполнения геометрических операций и формирования новых объектов. Будем обозначать в дальнейшем скаляры буквами греческого алфавита α,β,γ,..., точки — прописными буквами латинского алфавита P,Q,R,..., а векторы— строчными буквами латинского алфавита u,v,w,.... Позже, в разделе 4.3, будет введено в рассмотрение и другие абстрактные математические объекты. Их будем обозначать полужирными буквами латинского алфавита.

Сделаем важное замечание. Пока нет какой-либо системы координат векторы и точки можно рассматривать только как абстрактные объекты, а не как объекты, представленные в определенной системе отсчета. Тем не менее, с ними что-то можно делать и как то характеризовать.

Модуль вектора v (или его длина, абсолютная величина — magnitude) — это действительное число; его обозначим | v |. В этом случае можно выполнить операцию умножения скаляра на вектор -|α v |, причем она обладает следующим свойством

|α v | = |α|| v |.

Эту операцию часто называют масштабированием вектора.

При положительном α направление вектора α v то же, что и направление вектора v. Заметим, что имеет место специальный вектор нулевой длины (нуль-вектор — zero vector); его будем обозначать полужирной цифрой 0.

Для точек и векторов в АП существуют две эквивалентные операции. Они связывают две точки и вектор. Первая операция — это вычитание точек. Она формирует из двух точек Р и Q вектор v (рис. 6). Эту операцию запишем следующим образом:

v = P - Q.

 

 

Рис.6. Вычитание точек

 

Следствием такого определения операции вычитания точек является то, что для заданной точки Q и вектора v существует единственная точка Р, которая удовлетворяет приведенному выше соотношению. Это утверждение формально можно выразить так: пусть заданы точка Q и вектор v, тогда существует точка Р, такая, что

Р = v +Q.

 

 

 

Рис. 7. Слева – сложение векторов, справа – соотношение между точками

Таким образом, новый объект Р (точка) формируется с помощью операции сложения вектора с точкой. Правило соединения начала вектора с концом другого вектора позволяет наглядно представить операцию сложения векторов (рис. 7). Из правила сложения векторов следует и отношение, справедливое для любых трех точек P,Q и R

(P - Q) + (Q - R) = P - R.

Ø Формирование новых объектов (геометрических типов).

ü Прямые

Логическим следствием операции сложения точки и вектора (или, иначе, операции вычитания точек) есть понятие прямой в аффинном пространстве. Рассмотрим все точки, удовлетворяющие соотношению

Р(α) = P₀ + α d,

где Р₀ — произвольная точка, d — произвольный вектор, а α— некоторый скаляр. В соответствии с правилами объединения точек, векторов и скаляров, определенными в аффинном пространстве, Р(α) есть точка при любом заданном значении α. Все эти точки будут лежать на прямой, как показано на рис. 8. Такую форму представления прямой часто называют параметрической, так как совокупность точек, представляющих прямую, формируется в результате изменения значения параметра α.

При α = 0 - точка на прямой совпадает с точкой Р₀, и по мере увеличения α точки располагаются все дальше от исходной в направлении вектора d. Если ограничить значения параметра α только неотрицательными числами, то получим луч, исходящий из точки Р₀ в направлении вектора d.

 

Рис. 8 Определение прямой в АП

 

Ø Операция аффинного сложения. Линейные комбинации векторов.

В аффинном пространстве определены операции:

ü сложения двух векторов,

ü умножения вектора на скаляр (масштабирование) и

ü сложения вектора и точки,

но нет операции сложения произвольных точек и умножения точки на скаляр. Однако в этом пространстве определена такая операция аффинного сложения (affine addition), в которой имеются некоторые элементы двух последних операций. Так, для любой точки Q, вектора v и положительного скаляра «α» результат операции

Р = Q + αv

описывает все точки на прямой, проходящей через точку Q в направлении вектора v (рис. 4.8). И всегда можно найти такую точку R, что

v = R - Q.

Следовательно,

Р = Q + α(R - Q) = αR + (1 – α)Q

Эта операция выглядит так же, как и сложение двух точек, и, следовательно, имеет эквивалентную форму в виде:

P = α₁R + α₂Q,

где сумма

α₁ + α₂ = 1.

Таким образом, мы получили более широкое представление об операции аффинного сложения.

После введения правил сложения и масштабирования дадим определение линейной комбинации (linear combination) векторов.

Для создания линейной комбинации двух одной и той же размерности векторов w и v нужно масштабировать каждый из них с помощью скаляров, например a и b, и сложить эти взвешенные величины для создания нового вектора a v + b w. Этот вектор есть линейная комбинация двух заданных векторов.

Линейная комбинация может быть получена и для большего числа векторов.

Более общее определение: Линейной комбинацией m векторов v₁,v₂,…,v_m называется вектор вида

w = a₁ v₁ + a₂ v₂ + … + a_m v_m,

где a₁, a₂, … a_m – скаляры.

Для примера – линейная комбинация двух векторов 6(-1, 0, 2) и 2(3, 4, -1) дает новый вектор (0, 8,10). Проверьте. Так ли это?

Есть несколько видов линейных комбинаций.

Сейчас нас интересует понятие - Аффинные комбинации векторов.

Линейная комбинация называется аффинной (affine combination), если сумма коэффициентов

а₁ + а₂ + … + а_m = 1.

Например, 3 a +2 b – 4 с – аффинная комбинация векторов a, b и с, в то время как 3 a + b – 4 с - такой не является.

Коэффициенты линейной комбинации двух векторов a и b можно привести искусственно к тому, что бы их сумма стала равной 1. Для этого умножают один вектор на некоторый скаляр t, а второй на (1-t): (1-t) a + (t) b.

 

 

Ø Отрезки и выпуклость.

При 0 < α < 1 операция аффинного сложения определяет отрезок, связывающий точки R и Q, как показано на рис. 4.9.

Рис. 9. Отрезок прямой, соединяющий две точки.

 

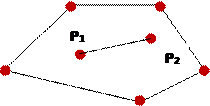
В компьютерной графике важным понятием служит понятие выпуклости объекта.

Говорят, что геометрический объект является выпуклым (convex), если все точки отрезка, соединяющего две любые точки внутренней области объекта, также принадлежат внутренней области.

Исходя из этого определения, можно заключить, что отрезок есть выпуклый объект и может быть построен в аффинном пространстве.

Более широкое понятие – это Выпуклые линейные аффинные комбинации векторов.

Выпуклая комбинация (convex combination) – есть дальнейшее ограничение линейной, для которой не только сумма коэффициентов должна быть равна 1, но и все коэффициенты должны быть положительными числами, т.е.

а₁ + а₂ + … + а_m = 1,

причем

a_i ≥ 0 для всех i = 1, 2…, m.

Это значит, что все a_i – должны находиться в интервале значений 0 и 1.

Совокупность коэффициентов а₁ + а₂ + … + а_m иногда называют разбиение единицы.

Пример выпуклой комбинации векторов a и b: 0,3 a + 0,7 b.

В некоторых случаях применяют понятие «множество всех выпуклых комбинаций» некоторого набора векторов. Для двух векторов v₁ и v₂ множество всех выпуклых комбинаций есть множество всех векторов вида:

v = (1 –α;) v₁ + α v₂,

где α; может изменяться от 0 до 1. Это равенство можно преобразовать к виду

v = v₁ + α;(v₂ – v₁).

Операцию аффинного сложения можно расширить на объекты, заданные рядом n точек P₁, P₂, …, P_n

P = α₁P₁ + α₂P₂ +... + α_nP_n

Это выражение справедливо, если сумма

α₁ + α₂ +... + α_n = 1.

Множество точек, образованных аффинным сложением n точек, на которое распространяется дополнительное ограничение

а_i > 0, i= 1,2,..., n,

- называют выпуклой оболочкой (convex hull) исходного набора точек (рис. 10). Такие точки могут лежать не обязательно на одной прямой. И могут образовать некоторую оболочку. По индукции доказывают, что выпуклая оболочка включает все отрезки прямых, связывающих любую пару точек из набора {Р₁ Р₂,..., Рn}.

 

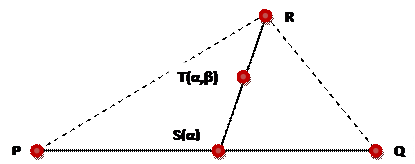
Рис. 10. Выпуклый многоугольник и выпуклый в нем отрезок

В геометрической трактовке выпуклая оболочка — это множество точек, принадлежащих поверхности минимальной площади, "натянутой" на заданное множество исходных точек. Понятие выпуклости играет особенно важную роль при конструировании кривых и поверхностей.

Ø Плоскости

Плоскость (plane) в аффинном пространстве определяют прямым расширением параметрического представления прямой. Из курса элементарной геометрии известно, что три точки, не лежащие на одной прямой, однозначно определяют плоскость.

Предположим, что P, Q и R — это именно такие три точки в аффинном пространстве. Отрезок, который соединяет P и Q, есть множество точек, описываемое соотношением

S(α) = αP + (1 – α)Q

Предположим, что в этом отрезке выбрана произвольная точка и из нее проведен отрезок до точки R, как показано на рис. 11. Точки, расположенные на этом отрезке, можно описать, воспользовавшись вторым параметром, β:

T(β) = βS + (1 – β)R

 

Рис. 11. Создание плоскости в аффинном пространстве

Эти точки определяются уже парой параметров — α и β, а их совокупность образует плоскость, заданную точками Р, Q и R. Объединив два предыдущих уравнения, получим уравнение плоскости в параметрическом виде:

Т(α,β) = β[αP + (1 – α)Q] + (1 – β)R

Полученное уравнение можно переписать в другом виде:

Т(α,β) = Р + β(1 – α)(Q -Р) + (1 – β)(R- P).

Учитывая, что Q-P и R-P представляют собой векторы, можно показать, что плоскость также определяется точкой Р₀ и парой непараллельных векторов u и v следующим образом:

Т(α,β) = Р₀ + αu + βv.

Теперь можно прийти к заключению, что при 0 < α, β < 1 все точки Т(α,β) лежат внутри треугольника, образованного вершинами P,Q и R. Если точка Р принадлежит плоскости, то

Р- Р₀ = αu + βv.

Можно определить вектор n, который будет ортогонален одновременно и u, и v. Воспользовавшись векторным произведением

n= u х v,

получим уравнение плоскости в таком виде:

n ∙ (Р-Р₀) = 0.

Вектор n перпендикулярен (ортогонален) плоскости; его принято называть нормалью к плоскости. Уравнения прямых, в левой части которых стоит член Р(α), и плоскостей, в левой части которых стоит член Т(α,β), принято называть уравнениями в параметрической форме, поскольку они определяют точки на прямой или плоскости как функции параметров α и β.