Основные законы массопередачи
В процессах переноса распределяемого компонента из одной фазы в другую различают два случая: 1) перенос из потока одной жидкости (газа) в поток другой жидкости или наоборот; 2) перенос из твердого тела в поток жидкости (газа) или в обратном направлении, т. е. массообмен между пористой твердой фазой и потоком жидкой (газообразной) фазы. Элементарными законами, которым подчиняется перенос распределяемого вещества из одной фазы в другую, являются законы молекулярной диффузии, массоотдачи и массопроводности. Закон молекулярной диффузии (первый закон Фика). Молекулярная диффузия в газах и растворах жидкостей происходит в результате хаотического движения молекул, не связанного с движением потоков жидкости. В этом случае происходит перенос молекул распределяемого компонента из областей высоких концентраций в область низких концентраций. Кинетика переноса подчиняется в этом случае первому закону Фика, формулировка которого аналогична закону теплопроводности: количество вещества, продиффундировавшего в пределах фазы, пропорционально градиенту концентраций, площади, перпендикулярной направлению диффузионного потока, и времени:
где
Коэффициент диффузии показывает, какое количество вещества диффундирует через поверхность 1 м2 в течение 1 с при разности концентраций на расстоянии 1 м, равной единице. Знак минус в правой части уравнения показывает, что при молекулярной диффузии направление перемещения вещества и градиент концентраций противоположны друг другу. Размерность коэффициента зависит от способа выражения концентрации распределяемого компонента. Если это объемные концентрации, то размерность коэффициента следующая:
Коэффициент диффузии не является постоянной величиной. Это достаточно малая величина для газов. Она на четыре порядка выше, чем для жидкостей. Коэффициент диффузии увеличивается с ростом температуры и уменьшается с повышением давления. Если в газах коэффициент диффузии не зависит от концентрации диффундирующего вещества, то в жидкостях это влияние особенно значимо для неразбавленных растворов. Дифференциальное уравнение молекулярной диффузии (второй закон Фика). Для вывода дифференциального уравнения, как это было принято для всех рассмотренных случаев в гидростатике и теплопроводности, выделяется в неподвижной среде элементарный параллелепипед с ребрами dx, dy, dz (рис. 1.8).
Рис. 1.8. К выводу дифференциального уравнения молекулярной диффузии
Если через этот элементарный параллелепипед за счет молекулярной диффузии перемещается распределяемое вещество, то через левую, заднюю и нижнюю грани за промежуток времени
При этом концентрация диффундирующего вещества повышается на Согласно основному уравнению молекулярной диффузии,
Следовательно,
Аналогично найдем
Суммируя левые и правые части трех последних равенств, получим:
С другой стороны, тот же прирост количества диффундирующего вещества в элементе можно найти умножением объема элемента на изменение концентрации за время
Приравнивая правые части двух последних зависимостей, получим уравнение молекулярной диффузии:
Левая часть этого уравнения характеризует локальное изменение концентрации распределяемого компонента в неподвижном элементе, выделенном в распределяющей фазе. Закон массоотдачи (Щукарева). Основной закон массоотдачи, или конвективной диффузии, впервые был сформулирован Щукаревым при изучении кинетики растворения твердых тел. Этот закон является аналогом закона теплоотдачи, сформулированного Ньютоном. Количество вещества, перенесенного от поверхности раздела фаз в воспринимающую фазу, пропорционально разности концентраций у поверхности раздела фаз и в ядре потока воспринимающей фазы, поверхности фазового контакта и времени:
где Отметим, что концентрация на границе Размерность коэффициента массоотдачи можно установить из уравнения
Коэффициент массоотдачи показывает, какое количество вещества передается от поверхности раздела фаз в воспринимающую фазу через поверхность в 1 м2 в течение 1 с при разности концентраций, равной единице. Для установившегося процесса коэффициент массоотдачи и концентрации сохраняют постоянное значение в рассматриваемом объеме:
Если коэффициент массоотдачи сохраняет постоянное значение для всей поверхности, то уравнение принимает вид
Дифференциальное уравнение массоотдачи (конвективной диффузии). Согласно этой теории распределяемое вещество переносится из ядра потока жидкости к границе раздела фаз непосредственно потоками жидкости и молекулярной диффузией (рис. 1.9). Рассматриваемая система состоит из двух частей: ядра и пограничного диффузионного слоя, включающего в себя достаточно тонкий ламинарный подслой. В ядре перенос вещества осуществляется преимущественно токами жидкости в условиях достаточной турбулентности. Концентрация распределяемого компонента в ядре турбулизированного потока фазы принимается постоянной (
Рис. 1.9. К формулировке закона конвективной диффузии
По мере приближения к пограничному диффузионному слою турбулентный перенос затухает и с приближением к границе раздела фаз в ламинарном подслое начинает превалировать перенос за счет молекулярной диффузии. Соответственно этому появляется градиент концентрации распределяемого компонента, увеличивающийся по мере приближения к границе. Таким образом, область диффузионного пограничного слоя – это область проявления и роста молекулярной диффузии от малого до максимального значения. При наличии конвективной диффузии концентрация распределяемого компонента изменяется не только вследствие молекулярной диффузии, но и механического переноса его из одной области пространства в другую. В этом случае концентрация распределяемого компонента будет функцией не только координат x, y, z и времени При конвективной диффузии бесконечно малый элемент потока перемещается из одной точки пространства в другую. В этом случае изменение концентрации распределяемого компонента может быть выражено субстанциональной производной, которая учитывает изменение ее во времени и изменения, связанные с перемещением элемента из одной точки пространства в другую:
В этом равенстве Если в уравнении молекулярной диффузии (1.17) заменить локальное изменение концентрации
Уравнение конвективной диффузии необходимо решать совместно с уравнениями движения Навье-Стокса, поскольку переменными являются концентрации и проекции скорости потока. Однако эта система уравнений не имеет аналитического решения, и для получения расчетных зависимостей по массообмену приходится прибегать к теории подобия.
|

 , (1.16)
, (1.16) – коэффициент пропорциональности, или коэффициент диффузии.
– коэффициент пропорциональности, или коэффициент диффузии.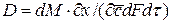
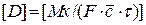 = [(кг·м·м3)/(м2·с·кг)] = [м2/с].
= [(кг·м·м3)/(м2·с·кг)] = [м2/с].
 в него входят количества вещества соответственно
в него входят количества вещества соответственно  и
и  , а через противоположные грани – правую, переднюю и верхнюю – входят количества вещества соответственно
, а через противоположные грани – правую, переднюю и верхнюю – входят количества вещества соответственно 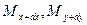 и
и 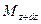 . Следовательно, элемент за промежуток времени
. Следовательно, элемент за промежуток времени  .
.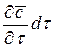 .
. ,
,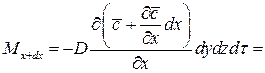
 .
. .
. ;
;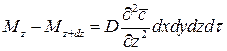 .
.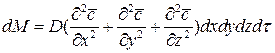 .
. .
.
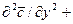
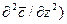 . (1.17)
. (1.17)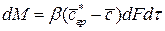 , (1.18)
, (1.18)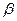 – коэффициент массоотдачи, характеризующий перенос вещества в пределах фазы конвекцией и диффузией одновременно;
– коэффициент массоотдачи, характеризующий перенос вещества в пределах фазы конвекцией и диффузией одновременно;  – концентрация распределяемого компонента у поверхности раздела распределяющей фазы;
– концентрация распределяемого компонента у поверхности раздела распределяющей фазы; 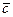 – концентрация распределяемого компонента в ядре потока распределяющей фазы.
– концентрация распределяемого компонента в ядре потока распределяющей фазы.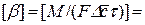 [(кг·м3)/(м2·с·кг)]=[м/с].
[(кг·м3)/(м2·с·кг)]=[м/с]. . (1.19)
. (1.19) . (1.20)
. (1.20)
 , но и составляющих скорости перемещения частиц потока
, но и составляющих скорости перемещения частиц потока  .
.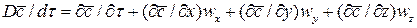 . (1.21)
. (1.21)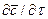 представляет собой локальное изменение концентрации распределяемого компонента, а комплекс
представляет собой локальное изменение концентрации распределяемого компонента, а комплекс 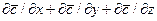 – конвективное изменение концентрации.
– конвективное изменение концентрации.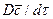 , в соответствие с уравнением (1.21), то можно получить дифференциальное уравнение конвективной диффузии:
, в соответствие с уравнением (1.21), то можно получить дифференциальное уравнение конвективной диффузии:
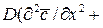

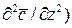 (1.22)
(1.22)


