Движущая сила массообменных процессов
Движущей силой массообменных процессов является разность между рабочей и равновесной концентрациями или наоборот. Это зависит от того, которая из указанных концентраций больше. На рис. 1.4 приведены возможные варианты выражения движущей силы массообменного процесса при одном и том же направлении перехода распределяемого вещества. При этом движущую силу можно выражать либо через концентрации распределяемого вещества в фазе G, либо L. В этой связи уравнения массопередачи, записанные по фазам, имеют вид
Индексы у коэффициента скорости процесса
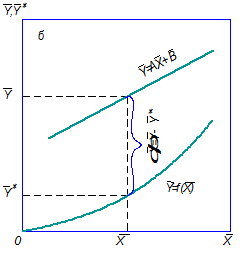
На рис. 1.4. показано, как движущая сила меняется с изменением рабочих концентраций. В этой связи для всего процесса массообмена, протекающего в пределах изменения концентраций от начальных до конечных, должна быть определена средняя движущая сила по газовой фазе
а) б) Рис. 1.4. Движущая сила массообменного процесса для участка аппарата: а) по газовой фазе; б) по жидкой фазе
С учетом средней движущей силы процесса основное уравнение массопередачи для всей поверхности контакта фаз может быть записано в виде
При определении движущей силы возможны два случая: – зависимость между равновесными концентрациями не линейна и определяется функциональной зависимостью самого общего вида типа – зависимость между равновесными концентрациями линейная – Определим среднюю движущую силу по фазе G для случая перехода распределяемого компонента из газовой в жидкую фазу. Для элемента поверхности имеем
Из сопоставления предыдущих равенств получим
для элементарной поверхности фазового контакта имеем
После интегрирования в пределах 0 – F и
Изменим границы интегрирования с целью исключения отрицательного знака перед интегралом и вставим равенство для
При выражении движущей силы для жидкой фазы получим аналогичное выражение:
При сравнении уравнений (1.9) и (1.10) с уравнениями (1.12) и (1.13) составим выражения для средних движущих сил по газовой и жидкой фазам:
Интегралы, стоящие в правой части равенств (1.14) и (1.15), называют числами единиц переноса – сокращенно ЧЕП. Отсюда выражение для ЧЕП в газовой фазе имеет
а выражение для ЧЕП в жидкой фазе:
Число единиц переноса, как следует из уравнений (1.14) и (1.15), можно определять по средней движущей силе процесса:
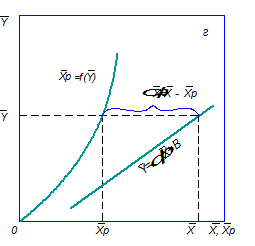
Физический смысл ЧЕП состоит в том, что эта величина характеризует изменение рабочей концентрации фазы, приходящееся на единицу движущей силы. Эти соотношения справедливы для всех случаев, когда между рабочими и равновесными концентрациями имеют место линейные и нелинейные зависимости. Числа единиц переноса выражаются интегралами, которые не могут быть решены аналитически, так как вид функции При графическом интегрировании (рис. 1.5) задаются рядом значений
Рис. 1.5. К расчету числа единиц переноса методом графического
Строят кривую зависимости
Аналогично, пользуясь графиком зависимости Для случаев, когда между равновесными концентрациями существует прямолинейная зависимость, при определении средней движущей силы используются более простые зависимости, вывод которых приведен в учебной литературе. Например, при расположении рабочей линии процесса выше линии равновесной для газовой и жидкой фаз зависимости для расчета средней движущей силы имеют вид
а для вычисления ЧЕП:
где
|

 ,
,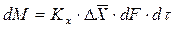 . (1.7)
. (1.7)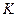 показывают, какие концентрации приняты для выражения движущей силы. В общем случае
показывают, какие концентрации приняты для выражения движущей силы. В общем случае  и
и 
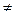
 , но всегда выполняется равенство
, но всегда выполняется равенство . (1.8)
. (1.8)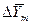 или жидкой –
или жидкой –  .
.

 , (1.9)
, (1.9)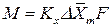 . (1.10)
. (1.10) ;
;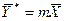
 – представляет собой постоянную величину).
– представляет собой постоянную величину).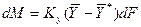 ;
; 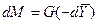 .
.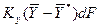

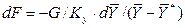 .
.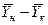 получим
получим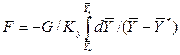 . (1.11)
. (1.11) :
: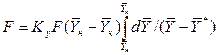 . (1.12)
. (1.12) . (1.13)
. (1.13) , (1.14)
, (1.14)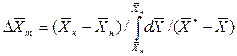 . (1.15)
. (1.15) ,
,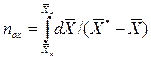 .
.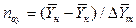 ,
, .
.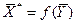 в каждом конкретном случае различен. В связи с этим число единиц переноса
в каждом конкретном случае различен. В связи с этим число единиц переноса 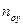 и
и 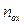 определяют методом графического или численного интегрирования.
определяют методом графического или численного интегрирования. , промежуточных между величинами
, промежуточных между величинами  и
и 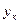 .
.
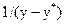 от
от  , заштрихованная на рисунке). После этого находят величину искомого интеграла с учетом масштабов
, заштрихованная на рисунке). После этого находят величину искомого интеграла с учетом масштабов 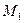 и
и  осей ординат и абсцисс:
осей ординат и абсцисс: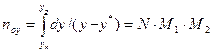 .
.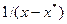 от
от  , определяют величину
, определяют величину 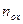 .
. ;
;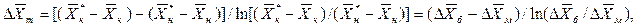
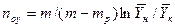 ;
; ,
, и
и 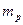 – тангенсы угла наклона рабочих и равновесных линий изменения концентраций.
– тангенсы угла наклона рабочих и равновесных линий изменения концентраций.


