Связь коэффициентов массопередачи и массоотдачи
Чтобы установить аналитическую зависимость между коэффициентами массопередачи и массоотдачи, принимают, что на границе раздела фаз достигается равновесие. Это предположение равносильно допущению о том, что сопротивлением переносу вещества через границу раздела фаз можно пренебречь. Отсюда как следствие вытекает положение об аддитивности фазовых сопротивлений, которое является одной из предпосылок к расчету коэффициента массопередачи. Допустим, что распределяемый компонент переходит из фазы G в фазу L и движущая сила выражается в концентрациях фазы G. При установившемся процессе массопередачи количество вещества, переходящее из одной фазы в другую фазу, определяется по уравнению
Для упрощения рассмотрим случай, когда равновесная зависимость между равновесными концентрациями представляет линейную зависимость Из уравнения равновесия следует
Уравнение массоотдачи для жидкой фазы
Подставляя значения
откуда
Из уравнения массоотдачи для газовой фазы
получим
Складывая выражения (1.23) и (1.24) и исключая неизвестную концентрацию на границе раздела фаз, получим
Из уравнения массопередачи следует, что
Приравнивая правые части и сокращая подобные члены, получим выражение для коэффициента массопередачи по газовой фазе:
При выражении коэффициента массопередачи в концентрациях жидкой фазы получим
Левые части уравнений представляют собой общее сопротивление переносу вещества из фазы в фазу, т. е. сопротивление массопередаче, а правые части – сумму сопротивлений массоотдаче в фазах. Поэтому эти зависимости являются уравнениями аддитивности фазовых сопротивлений. Эти уравнения справедливы и для случая, если линия равновесия является кривой.
|

 .
.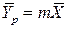 , где m – тангенс угла наклона линии равновесия.
, где m – тангенс угла наклона линии равновесия. и
и 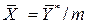 .
. .
.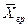 и
и 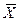 в уравнение массоотдачи, получим
в уравнение массоотдачи, получим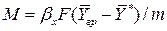 ,
,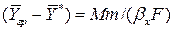 . (1.23)
. (1.23)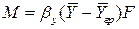
 . (1.24)
. (1.24)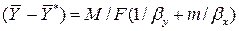 .
.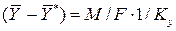 .
. . (1.25)
. (1.25) . (1.26)
. (1.26)


