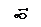
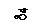
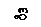
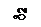
 Примером данного типа соединений служит крепление крышки резервуара, находящегося под давлением
Примером данного типа соединений служит крепление крышки резервуара, находящегося под давлением 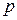 жидкости или газа (рисунок 1.3). Полная сила
жидкости или газа (рисунок 1.3). Полная сила  , Н, растягивающая болты (винты) при действии расчетного давления
, Н, растягивающая болты (винты) при действии расчетного давления 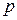 , Н/мм2, складывается из силы давления среды на крышку и остаточной силы, потребной для сжатия прокладки:
, Н/мм2, складывается из силы давления среды на крышку и остаточной силы, потребной для сжатия прокладки:
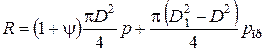 ,
,
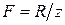 , (1.9)
, (1.9)
где 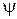 – коэффициент, учитывающий возможное повышение давления (обычно
– коэффициент, учитывающий возможное повышение давления (обычно 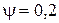 );
); 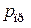 – давление на прокладке, Н/мм2, принимаемое для мягких прокладок равным
– давление на прокладке, Н/мм2, принимаемое для мягких прокладок равным 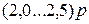 , а для металлических прокладок –
, а для металлических прокладок – 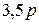 ;
; 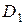 и
и 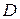 – соответственно наружный и внутренний (в данном случае равен внутреннему диаметру резервуара) диаметры прокладки, мм;
– соответственно наружный и внутренний (в данном случае равен внутреннему диаметру резервуара) диаметры прокладки, мм; 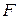 – внешняя осевая сила, приходящейся на один болт, Н;
– внешняя осевая сила, приходящейся на один болт, Н; 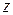 – число болтов.
– число болтов.
Затяжка болтов должна обеспечить герметичность соединения или нераскрытие стыка под нагрузкой.
После приложения внешней нагрузки 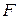 , приходящейся на один болт, к затянутому соединению болт дополнительно растянется на некоторую величину
, приходящейся на один болт, к затянутому соединению болт дополнительно растянется на некоторую величину 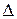 , а деформация сжатия деталей уменьшится на ту же величину. Для простоты можно считать, что часть внешней нагрузки дополнительно нагружает болт, а другая часть идет на разгрузку (раскрытие) стыка. Тогда дополнительная нагрузка болта равна
, а деформация сжатия деталей уменьшится на ту же величину. Для простоты можно считать, что часть внешней нагрузки дополнительно нагружает болт, а другая часть идет на разгрузку (раскрытие) стыка. Тогда дополнительная нагрузка болта равна 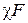 (
( – коэффициент внешней нагрузки, учитывающий приращение нагрузки болта), а уменьшение затяжки стыка –
– коэффициент внешней нагрузки, учитывающий приращение нагрузки болта), а уменьшение затяжки стыка – 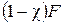 .
.
Значение коэффициента  определяют из условия совместности деформаций (т.е. по условию равенства дополнительных деформаций болта и деталей):
определяют из условия совместности деформаций (т.е. по условию равенства дополнительных деформаций болта и деталей):
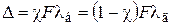 , (1.10)
, (1.10)
где 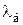 – коэффициент податливости болта, мм/Н;
– коэффициент податливости болта, мм/Н; 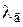 – суммарный коэффициент податливости соединяемых деталей, мм/Н.
– суммарный коэффициент податливости соединяемых деталей, мм/Н.
Из равенства (1.10) имеем
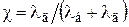 .
.
Для болтов постоянного сечения
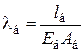 ,
,
где 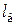 – длина болта, мм;
– длина болта, мм; 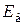 – модуль продольной упругости материала болта, Н/мм2;
– модуль продольной упругости материала болта, Н/мм2; 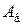 – площадь поперечного сечения болта, мм2.
– площадь поперечного сечения болта, мм2.
Для болтов переменного сечения
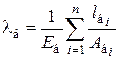 ,
,
где 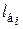 – длина
– длина 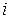 -го участка болта, мм;
-го участка болта, мм; 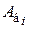 – площадь поперечного сечения
– площадь поперечного сечения 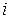 -го участка болта, мм2.
-го участка болта, мм2.
Суммарный коэффициент податливости деталей
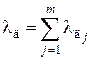 ,
, 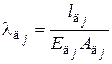 , (1.11)
, (1.11)
где 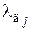 – коэффициент податливости
– коэффициент податливости 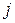 -ой детали, мм/Н;
-ой детали, мм/Н; 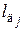 – толщина
– толщина 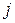 -ой детали, мм;
-ой детали, мм; 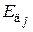 – модуль продольной упругости материала
– модуль продольной упругости материала 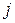 -ой детали, Н/мм2;
-ой детали, Н/мм2; 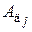 – расчетная площадь поперечного сечения
– расчетная площадь поперечного сечения 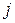 -ой детали, мм2.
-ой детали, мм2.
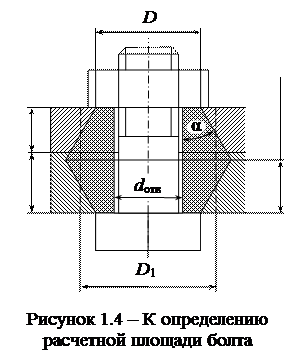
В формуле (1.11) под расчетной площадью 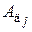 понимают площадь только той части детали, которая участвует в деформации от затяжки болта. Полагают, что деформации от гайки и головки болта распространяются в глубь деталей по конусам (рисунок 1.4) с углом
понимают площадь только той части детали, которая участвует в деформации от затяжки болта. Полагают, что деформации от гайки и головки болта распространяются в глубь деталей по конусам (рисунок 1.4) с углом 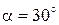 (
(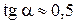 ). Объемы этих конусов приравнивают к объему цилиндра с диаметром
). Объемы этих конусов приравнивают к объему цилиндра с диаметром
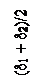
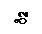
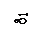
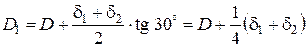 .
.
Тогда расчетная площадь будет определяться по формуле
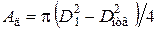 .
.
Из условия сохранения плотности стыка сила предварительной затяжки
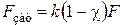 ,
,
где 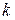 – коэффициент затяжки.
– коэффициент затяжки.
По условию нераскрытия стыка коэффициент затяжки принимается равным следующим значениям:
· при постоянной нагрузке 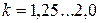 ;
;
· при переменной нагрузке 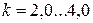 .
.
По условию герметичности соединения:
· при мягкой прокладке 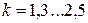 ;
;
· при металлической фасонной прокладке 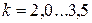 ;
;
· при металлической плоской прокладке 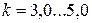 .
.
Расчетная осевая сила 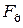 , Н, действующая на затянутый болт, после приложения внешней нагрузки
, Н, действующая на затянутый болт, после приложения внешней нагрузки 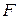 (см. формулу 1.9) будет определяться по формуле
(см. формулу 1.9) будет определяться по формуле
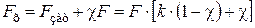 . (1.12)
. (1.12)
При приближенных расчетах для соединений из стальных деталей без мягкой прокладки 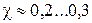 .
.
Предварительно определив значение расчетной осевой силы по формуле (1.12), затем при статической нагрузке определяют внутренний диаметр резьбы 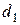 по формуле (1.3). По найденному значению
по формуле (1.3). По найденному значению 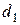 подбирают стандартный болт (винт) по таблице (1.1).
подбирают стандартный болт (винт) по таблице (1.1).
Примечание – Правильнее крутящий момент затяжки учитывать при определении расчетной осевой силы 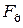 (поскольку внешняя осевая сила не создает момента затяжки):
(поскольку внешняя осевая сила не создает момента затяжки):
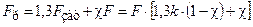 ,
,
далее определяют внутренний диаметр резьбы 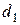 не по формуле (1.3), а по формуле (1.2), при этом в данную формулу вместо осевой силы F необходимо подставить найденное значение расчетной осевой силы
не по формуле (1.3), а по формуле (1.2), при этом в данную формулу вместо осевой силы F необходимо подставить найденное значение расчетной осевой силы 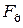 .
.
При переменной нагрузке определяется коэффициент запаса прочности
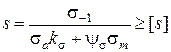 , (1.13)
, (1.13)
где 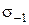 – предел выносливости материала болта при симметричном цикле изменения напряжений (таблица 1.1), МПа;
– предел выносливости материала болта при симметричном цикле изменения напряжений (таблица 1.1), МПа; 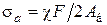 – амплитуда цикла напряжений, МПа;
– амплитуда цикла напряжений, МПа; 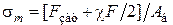 – постоянная составляющая цикла напряжений, МПа;
– постоянная составляющая цикла напряжений, МПа; 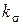 – эффективный коэффициент концентрации напряжений; для углеродистых сталей
– эффективный коэффициент концентрации напряжений; для углеродистых сталей 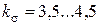 , для легированных сталей
, для легированных сталей 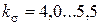 (большие значения при диаметре болта
(большие значения при диаметре болта 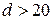 мм);
мм); 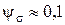 – коэффициент чувствительности к асимметрии цикла напряжений.
– коэффициент чувствительности к асимметрии цикла напряжений.

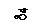
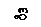
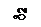
 Примером данного типа соединений служит крепление крышки резервуара, находящегося под давлением
Примером данного типа соединений служит крепление крышки резервуара, находящегося под давлением 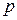 жидкости или газа (рисунок 1.3). Полная сила
жидкости или газа (рисунок 1.3). Полная сила  , Н, растягивающая болты (винты) при действии расчетного давления
, Н, растягивающая болты (винты) при действии расчетного давления 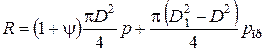 ,
,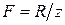 , (1.9)
, (1.9)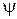 – коэффициент, учитывающий возможное повышение давления (обычно
– коэффициент, учитывающий возможное повышение давления (обычно 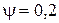 );
); 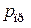 – давление на прокладке, Н/мм2, принимаемое для мягких прокладок равным
– давление на прокладке, Н/мм2, принимаемое для мягких прокладок равным 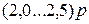 , а для металлических прокладок –
, а для металлических прокладок – 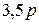 ;
; 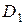 и
и 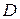 – соответственно наружный и внутренний (в данном случае равен внутреннему диаметру резервуара) диаметры прокладки, мм;
– соответственно наружный и внутренний (в данном случае равен внутреннему диаметру резервуара) диаметры прокладки, мм; 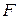 – внешняя осевая сила, приходящейся на один болт, Н;
– внешняя осевая сила, приходящейся на один болт, Н; 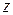 – число болтов.
– число болтов.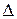 , а деформация сжатия деталей уменьшится на ту же величину. Для простоты можно считать, что часть внешней нагрузки дополнительно нагружает болт, а другая часть идет на разгрузку (раскрытие) стыка. Тогда дополнительная нагрузка болта равна
, а деформация сжатия деталей уменьшится на ту же величину. Для простоты можно считать, что часть внешней нагрузки дополнительно нагружает болт, а другая часть идет на разгрузку (раскрытие) стыка. Тогда дополнительная нагрузка болта равна 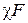 (
( – коэффициент внешней нагрузки, учитывающий приращение нагрузки болта), а уменьшение затяжки стыка –
– коэффициент внешней нагрузки, учитывающий приращение нагрузки болта), а уменьшение затяжки стыка – 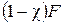 .
.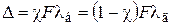 , (1.10)
, (1.10)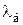 – коэффициент податливости болта, мм/Н;
– коэффициент податливости болта, мм/Н; 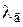 – суммарный коэффициент податливости соединяемых деталей, мм/Н.
– суммарный коэффициент податливости соединяемых деталей, мм/Н.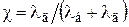 .
.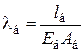 ,
,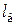 – длина болта, мм;
– длина болта, мм; 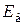 – модуль продольной упругости материала болта, Н/мм2;
– модуль продольной упругости материала болта, Н/мм2; 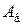 – площадь поперечного сечения болта, мм2.
– площадь поперечного сечения болта, мм2.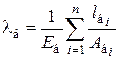 ,
,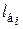 – длина
– длина 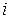 -го участка болта, мм;
-го участка болта, мм; 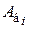 – площадь поперечного сечения
– площадь поперечного сечения 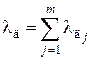 ,
, 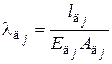 , (1.11)
, (1.11)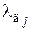 – коэффициент податливости
– коэффициент податливости 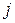 -ой детали, мм/Н;
-ой детали, мм/Н; 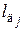 – толщина
– толщина 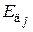 – модуль продольной упругости материала
– модуль продольной упругости материала 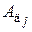 – расчетная площадь поперечного сечения
– расчетная площадь поперечного сечения 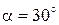 (
(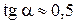 ). Объемы этих конусов приравнивают к объему цилиндра с диаметром
). Объемы этих конусов приравнивают к объему цилиндра с диаметром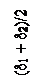
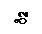
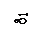

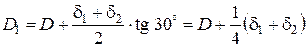 .
.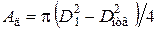 .
.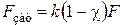 ,
,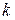 – коэффициент затяжки.
– коэффициент затяжки.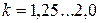 ;
;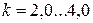 .
.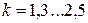 ;
;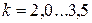 ;
;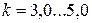 .
.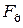 , Н, действующая на затянутый болт, после приложения внешней нагрузки
, Н, действующая на затянутый болт, после приложения внешней нагрузки 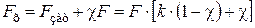 . (1.12)
. (1.12)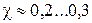 .
.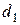 по формуле (1.3). По найденному значению
по формуле (1.3). По найденному значению 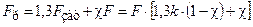 ,
,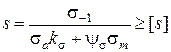 , (1.13)
, (1.13)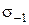 – предел выносливости материала болта при симметричном цикле изменения напряжений (таблица 1.1), МПа;
– предел выносливости материала болта при симметричном цикле изменения напряжений (таблица 1.1), МПа; 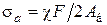 – амплитуда цикла напряжений, МПа;
– амплитуда цикла напряжений, МПа; 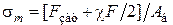 – постоянная составляющая цикла напряжений, МПа;
– постоянная составляющая цикла напряжений, МПа; 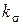 – эффективный коэффициент концентрации напряжений; для углеродистых сталей
– эффективный коэффициент концентрации напряжений; для углеродистых сталей 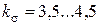 , для легированных сталей
, для легированных сталей 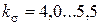 (большие значения при диаметре болта
(большие значения при диаметре болта 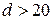 мм);
мм); 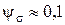 – коэффициент чувствительности к асимметрии цикла напряжений.
– коэффициент чувствительности к асимметрии цикла напряжений.


