Расчет клеммовых соединений на прочность
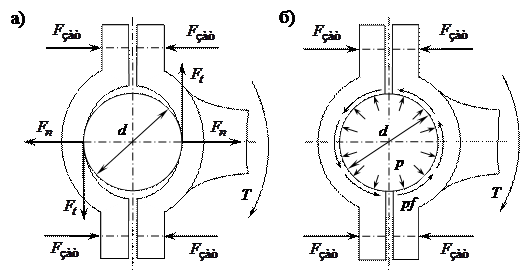
При проектировании соединения обычно требуется определить силу затяжки болтов, обеспечивающую взаимную фиксацию деталей и передачу требуемого вращающего момента и (или) восприятия осевой силы, а также оценить прочность болта (болтов) и охватывающей детали (клеммы). В зависимости от выполнения соединения при расчете на прочность рассматривают два предельных случая (рисунок 1.9).
Рисунок 1.9 – К расчету клеммовых соединений Первый расчетный случай. Клемма обладает высокой жесткостью, а посадка деталей выполнена с большим зазором (рисунок 1.9, а). В данном случае можно допустить, что контакт деталей происходит по линии. Тогда условие прочности соединения можно выразить в виде · при нагружении крутящим моментом
или
· при нагружении осевой силой
или
где По условию равновесия любой половины клеммы имеем
где Подставив значение
Второй расчетный случай. Клемма обладает высокой податливостью, посадочные поверхности соединяемых деталей – строго цилиндрические, зазор в соединении близок к нулю (рисунок 1.9, б). В данном случае предполагают, что давление · при нагружении крутящим моментом
или
· при нагружении осевой силой
или
где Из допущения о характере распределения сил взаимодействия по поверхности контакта следует, что если контакт осуществляется по поверхности полуцилиндра, то расчетная площадь
После подстановки (1.25) в формулы (1.23) и (1.24) определим необходимую силу затяжки болтов:
При совместном действии крутящего момента и осевой сдвигающей силы требуемая сила затяжки болтов определяется по формуле
Коэффициент трения для стальных и чугунных деталей, работающих без смазки, выбирается в пределах После определения требуемой силы затяжки по формулам (1.22) или (1.26) – (1.27) определяют диаметр резьбы болта по формуле (1.3) и подбирают стандартный болт. Для клеммового соединения с прорезью в ступице (рисунок 1.8, а) справедливы соотношения (1.26) и (1.27).
|

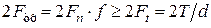 ,
,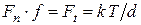 ; (1.20)
; (1.20) ,
,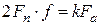 , (1.21)
, (1.21)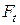 – окружное усилие, Н;
– окружное усилие, Н; 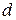 – диаметр вала (диаметр посадочной поверхности), мм;
– диаметр вала (диаметр посадочной поверхности), мм; 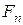 – нормальная реакция в месте контакта, Н;
– нормальная реакция в месте контакта, Н; 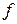 – коэффициент трения;
– коэффициент трения; 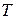 – крутящий момент, Н·мм;
– крутящий момент, Н·мм; 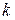 – коэффициент запаса сцепления.
– коэффициент запаса сцепления.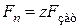 ;
;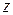 – число болтов.
– число болтов.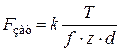 ,
, 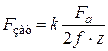 , (1.22)
, (1.22)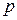 , МПа, равномерно распределено по посадочной поверхности соприкасающихся деталей (как в соединениях с натягом). Условия прочности соединения при действии сдвигающей нагрузки (крутящего момента или осевой силы) имеют вид
, МПа, равномерно распределено по посадочной поверхности соприкасающихся деталей (как в соединениях с натягом). Условия прочности соединения при действии сдвигающей нагрузки (крутящего момента или осевой силы) имеют вид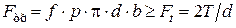 ,
,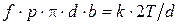 ; (1.23)
; (1.23)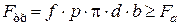 ,
,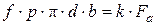 , (1.24)
, (1.24)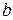 – длина ступицы клеммы (длина посадочной поверхности), мм.
– длина ступицы клеммы (длина посадочной поверхности), мм.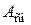 равна площади проекции поверхности контакта на диаметральную плоскость (произведению диаметра цилиндрической поверхности на ее длину). В соответствии с этим, если соединение имеет
равна площади проекции поверхности контакта на диаметральную плоскость (произведению диаметра цилиндрической поверхности на ее длину). В соответствии с этим, если соединение имеет 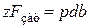 . (1.25)
. (1.25) ,
, 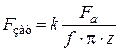 . (1.26)
. (1.26)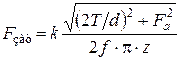 . (1.27)
. (1.27) . Коэффициент запаса сцепления
. Коэффициент запаса сцепления 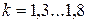 .
.


