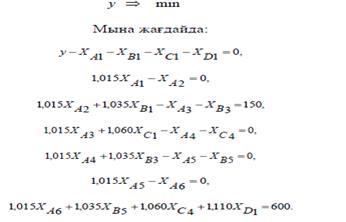Ма'сатты' 'аржылы' 'орды 'Cру есебі
Ақшаны өсім пайызына салудың əртүрлі тəсілдері жəне əдістері болатыны бүгінгі кезде əркімге белгілі. Сөзсіз, кім де болса өсім пайызына ақшаны минимальды мөлшерде салып, максималь- ды табыс немесе пайда табуға тырысады. Сондықтан, салымнан максимальды табыс алу үшін, оны іске қандай тəсіл жəне əдіспен салған тиімді деген еріксіз сұрақ туады. Тəжірибеде мұндай есептерді қаржыларды жоспарлау есебі деп атайды. Есепте өте маңызды жəне күрделі мəселелердің бірі тəуекелділік (риск) көрсеткішінің мəнін дəйектеу жəне анықтау. Сонымен қатар басқа да факторлардың өсімге салған қаражатқа əсерін нақтылы дұрыс анықтаған маңызды. Қарастырылып отырған есепті ретке келтіру мақсатында (формализация) мынадай сөздіктерді енгізейік: – салым – іске салған ақша; – алдын-ала жиналған ақша – мақсаттық қаржылық қор; – салым бойынша тəуекелділік (риск) индексі. Тəжірибеде қаржыларды жоспарлау есебінің бірнеше нұсқа- лары кездеседі. Біз мақсаттық қаржылық қорды минимальды мөлшерде іздеу деп аталатын қаржыларды жоспарлау есебінің А– нұсқасын қарастырамыз. Айталық, бір мезгілде салымға салған немесе несиеге беруші қарызға берген қаражатты қайтару керек, яғни қарызгер немесе банк нақтылы бір соманы төлеуге тиіс. Осы соманы төлеу үшін қарызгер немесе банк алдын-ала бір қаражатты жинақтайды. Осындай мақсатта жинақталған қаражатты мақсаттық қор деп атаймыз. Салым қысқа мерзімге салынсын. Бұл жерде қысқа мерзімдік деп салымның салған уақытымен оны қайтарған уақыт аралығы айтылады жəне осы мерзімде салымнан түскен табыс та анықталуға тиіс. Сонымен, есептің мақсаты мақсаттық қордың минимальды мөлшерін анықтайтын жəне қарызды өтеуге жұмсалатын салым түрлерін таңдау. Оқылып, зерделенетін көрсеткіштерді мынадай символдармен белгілейік: Y – бір мақсат үшін алғашқы салынған салым мөлшері (қаржыландыру əрекетінің басында уақыт мезгілі нөлге тең деп есептелінеді, t = 0); t – ағымдағы уақыт белгісі (t = 0, 1, …, T); Ct – t - уақытта (t = 1, 2, …, T) төленген ақша мөлшері; j – тез мерзімді салым индексі, j= 1, 2, …, n; vj – тез мерзімді j - салымның салынған уақыты; wj – тез мерзімді j - салым бойынша қаражатты қайтару мерзімі; rj – тез мерзімді j - салымнан алынатын табыс; xj – тез мерзімді j - салымның алғашқы мөлшері. T– займды (салымды қанша жылға, уақытқа) берген мерзімнің мөлшері; n – салымдар саны. Кез келген тез мерзімді j салым vj уақытта салынған мөлше- рі белгілі жəне ол есепке алынған деп санайық. Егер тез мерзімде j салымның алғашқы мөлшері xj болса, онда wj – қаражатты қайтару мерзімінде банк немесе несиеге алушы (қарызгер) мына мөлшерде (1+ rj) xj ақшаны клиентке қайтаруға міндетті. Қоғамда болып жатқан əртүрлі шектеулер ескерілмей, кез келген уақыт мезгілінде төлей алатындай салым салынған деп есептейік. Кез келген уақыт мезгілінде төлей алатын салымдардың табысы нөлге тең болуы мүмкін. Нөлдік табысты салымды қолдану ақша активтенбегендігін көрсетеді, яғни мағынасы ақша иесінің қолында қалғанмен бірдей. Осындай талдау жүргізе отырып, əрі қарай есепті қалыптас- тыра беру үшін, тағы да мынадай символдарды енгізейік. Айталық, j Gt немесе j = 1, 2, …, Gt, мұндағы Gt – t – уақыт мезгіліндегі салымшылар саны, олай болса бұл көптік тек уақыт t= v j, яғни j – ші салымға t уақыт мезгілінде ақша салынған. Демек, ақшаны қайтару əрекетін де осындай символдармен белгілеп, аламыз: j Qt немесе j = 1, 2, …, Q t, мұндағы Q t – t - уақыт мезгіліндегі төленген салымдар саны, яғни мына уақыт t = v j+ w j мерзімінде j - ші салым өтелген. Сөйтіп, кез келген t- уақыт мезгілінде Gt жəне Q t белгілі болатынын байқаймыз. Жоғарыдағы қабылданған символдарды қолданып, есептің математикалық моделін жазайық: min ⇒ n j j y x (8.8) Мына жағдайда: 0, 0, j Gt y x j t (8.9) (1), 1, 1, j Qt Bt t T t j G r j x j x j (8.10) j Qt (1 r j) x j Ct, t T, (8.11) y 0, x j 0, j 1,2,..., n. (8.12) Математикалық модельдегі (8.8) формула мақсаттық қаржы- лық қордың минимальды мəнін іздейтін мақсат функциясы. Атал- ған функцияның минимальды мəні қаржы əрекеттерінің барлық талабының орындалуын қамтамасыз етуге тиіс, яғни мынадай жағ- дайларда: – қаржы əрекеттері əлі басталған жоқ, яғни уақыт мезгілі нөлге тең, ал мақсаттық қор салымдарға бөлінген жəне барлық салымдардағы сомамен мақсаттық қордың айрымы нөлге тең (8.9– ші шектеу); – төленген сомалармен салымдар сомаларының баланыстық қатынасын көрсететін шектеу (8.10–ші шектеу). Формуладағы B t – – t - уақыт мезгіліндегі пайыздық ақша мөлшері немесе табыс мөлшері; – пайыздық ақшаларымен қоса салымшыларға төленген қаржы мөлшері немесе займға алынған қаражатты қойылған мерзі- мінде өтеуді қамтамасыздандыру шарты (8.11–ші шектеу); – мақсаттық қорды құру жəне салымға ақшаны салу тиімді немесе тиімсіз, яғни математикалық тілде айнымалылардың теріс болмау шарты (8.12–ші шектеу). Табыстың максимльды мəнін іздейтін қаржыны жоспарлау есебінің тағы бір нұсқасын (В нұсқасы) қарастырайық. Айталық, са- лымшы бір уақыт аралықтарында максимальды пайда табу үшін, қаражатын салымға салсын. Есеп мақсаттық қордың бекітілген бел- гілі бір мөлшерінде, барлық тез мерзімдік салымдар ішінен макси- мальды табысты қамтамасыз ететіндерін таңдап алу керек. Жоғарыдағы келтірілген символдармен қатар тағы да мына- дай белгілерді қабылдайық: Bt – салымшылардың T- уақыт мезгілінде алған табысы; At – t - уақыт мезгілдерінде салынған салым мөлшерлері (t = 1, 2, …, T). Келесі кезекте есептің математикалық моделін тұрғызайық. Табыс максимальды болуын көрсететін мақсат функция: (1) max, 1, 1, ⇒ j Qt t T t j G Bt r j x j x j (8.13) Мына жағдайда: – бастапқы уақыт мезгілінде мақсаттық қордың салымдар бойынша бөлінуін сипаттайтын шарт: , 0, j Gt x j At t (8.14) – төленген сомалармен салымдар сомаларының баланыс- тық қатынасын көрсететін шарт: (1), 1, 1, j Qt r j x j At t T t j G x j (8.15) – табыс шамасын анықтайтын шарт: (1) 0, 1,, j Qt r j x j Bt t T (8.16) – ешқандай табыс ала алмаймыз немесе аламыз жəне са- лымға ақшаны салу тиімді немесе тиімсіз, яғни математикалық тілде айнымалылардың теріс болмау шарты: Bt 0, x j 0, j 1,2,..., n.; t 0,1,2,..., T. (8.17) 1. Ақшаны пайыздық үстемеге салу. Фермер көксөкті сақтауға арналған құралды сатып алу үшін, осы құралды шыға- ратын кəсіпорынмен келісім-шартқа отырды. Құралды өндіріске қоятын кəсіпорынға келісім-шарт бойын- ша фермер 750 млн. теңге төлеуге тиіс. Келісім шартта бірінші екі ай өткеннен кейін 150 млн. теңге, ал қалған 600 млн. теңгені алты айдан соң, құралды өндіріске енгізгізіп, сынақтан өткізгеннен кейін төлеу керектігі көрсетілген. 8.4–кесте. Салым салу тəсілдеріні_ алғаш_ы мəліметтері Салым салу нұсқалары Салым ұзақтығы, ай Салым салу уақыты мезгілдері (ай басы) Пайыздық үстемесі, % А 1 1,2,3,4,5,6 1,5 В 2 1,3,5 3,5 С 3 1,4 6,0 D 6 1 11,0 Фермер келісім-шарт жасалған күннен бастап мақсат қорын жинақтауға кірісті. Мақсат қор жинақталғаннан кейін қаражатты белсендіру үшін (активтендіру), ол депозитке қойылмақшы. Сөзсіз, мұндай іс–əрекет фермердің қаражатын өсірудің бір тəсілі. Мақ- саттық қор фермер сатып алатын құралдың құнынан (750 млн. теңгеден) айтарлықтай аз болуы керектігін жақсы түсінеді. Деген- мен, құралдың құнын толық төлеген кездің өзінде, өсім салымына қойған қаражат, оған бір шама көп те болуы мүмкін. Бірақ, фермердің инвестрлік мүмкіншілігі келісім-шартта көрсетілген əрекеттердің уақытында орындалуын қамтамасыздандыра ала ма? Мүмкін мақсаттық қор көпте болар, онда фермерге оны салымға қою тиімсіз болуы да мүмкін. Сөйтіп, мақсат қорын құрып, ақша- ны инвестрлеудің бірнеше нұсқалары (есепте A, B, C, D (8.4–кесте)) бар екеніне көз жеткізуге болады. Фермер барлық мүмкін бола алатын нұсқалардың (есепте келтірілген нұсқаларды бір–бірімен байланыста қарастырса 60-тан астам жаңа нұсқаларды алуға болады) ішінен ақшаны салымға пайыздық үстемемен қою-дың 12 тəсіліне тоқталды делік. Салым нұсқасы, олардың ұзақ-тығы, салым салу уақыты жəне пайыздық үстемесі 8.4 жəне 8.5–кестелерде келтірілген. Кестедегі келтірілген деректер бойынша __ралды_ __нын тHлеуді _амтамасыз ететін ма_сатты_ _орды_ мHлшерін мини- мальдау керек. СHйтіп, мынадай с_ра_тар туады: – құралдың толық құнын шартта көрсетілген уақытта төлеуді қамтамасыз ететін мақсаттық қордың мөлшері қанша болуы тиіс? – уақыт мезгілінің бас кезінде, жетінші айдың басында (6–ай біткеннен кейін) төленетін ақшаның бір теңгесінің бағасы қанша? – уақыт мезгілінің бас кезінде, бесінші айдың басында (4–ай біткеннен кейін) төленетін ақшаның бір теңгесінің бағасы қанша? 8.5–кесте. Салым салу жəне қаражатты қайтару мүмкіндіктері туралы деректер (үлестік коэффициенттері) Салым Айлар (осы айларды_ бірінші к<ні) 1 2 3 4 5 6 7 А, 1–айда 1,00 1,015 А, 2–айда 1,00 1,015 А, 3–айда 1,00 1,015 А, 4–айда 1,00 1,015 А, 5–айда 1,00 1,015 А, 6–айда 1,00 1,015 В, 1–айда 1,00 1,035 В, 3–айда 1,00 1,035 В, 5–айда 1,00 1,035 С, 1–айда 1,00 1,06 С, 4–айда 1,00 1,06 D, 1–айда 1,00 1,11 Ескерту: Кестеде жолдар бойынша бір н<с_ада а_шаны пайызды_<стемеге салу (коэффициенті 1,00 те_) жəне _айтару (коэффициенті, пайызды_ <стеме (8.4–кестені _ара_ыз) жəне _осылған бір) əрекеттерді_коэффициенттері келтірілген. Шешімі. Келесідей белгілерді енгізейік: y – мақсаттық қордың мөлшері; xAi – i- айында салынатын А-нұсқасындағы салым мөлшері; xBi – i- айында салынатын B-нұсқасындағы салым мөлшері; xCi – i- айында салынатын C-нұсқасындағы салым мөлшері; xDi – i- айында салынатын D-нұсқасындағы салым мөлшері; Ақшаны қолда сақтау ешқандай да пайда түсірмейді, сон- дықтан қолға ақша түссе кез келген айда оны пайыздық үстемемен іске саламыз. Осы жағдайды ескеріп жəне 8.5–кестедегі деректер бойынша мақсаттық қорды минимальдау есебінің моделі төменгідей түрде жазылады: Мақсат функция:
|