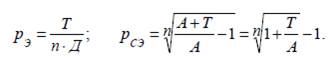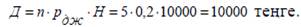БЕЛГІЛІСХЕМАЛАРАРҚЫЛЫCСУДАЛАРДЫБЕРГЕНДЕГІҚАРЖЫЛЫҚ ƏРЕКЕТТЕРДІҢНАЛОГИЯСЫ.
Бір t – уақытмезгіліндегі (жылмен) C ақшабірліктерініңсомасынантұратынкапиталды C(t) символыменбелгілейік. 5.1. Анықтама. Қаржылық əрекеттер деп t 1 уақытмезгілініңбасынан t2 уақытмезгілініңсоңынадейінгі (t2 > t 1) кезкелгеніс–əрекеттің (немесеешқандайіс–əрекетсіз) əсерінен C 1(t1) капиталдың C2 (t2) капиталғаайналуынайтады. 5.2. А н ы қ т а м а. Капитал C 1 инвестиция деп аталса, алкапитал C2 қаржылық əрекеттердің нəтижесі делінеді. 5.3. А н ы қ т а м а. Қаржылық əрекеттерде капиталдың үлкеюі коэффициенті дегеніміз нəтиженің инвестицияға қатынасы, яғни C2 / C1, ал қаржылық əрекеттерде номиналды табыс дегенімізнəтиже мен инвестиция айырымы, яғни C2 – C1. Қаржылық əрекеттерде табыстылық туралы түсініктіқарастырайық. Ол үшін ссудалар беру бойынша есептеуəрекеттерінің формулаларын еске түсірейік. Айталық p1, p2, p3 –сəйкесінше, қарапайым, күрделі жəне үздіксіз пайыздардыңт жылдық пайыздық үстемелері. Осы символдар бойынша пайыздарға арттыру формуласы мына түрде жазылады:
Осыдан, A, C жəне t шамалары белгілі деп есептеп, жылдық ипайыздық үстемелердің мəндерін табамыз:
Жоғарыдағы келтірілген формулалар табыстылы қ түсінігінің үш түрлі нұсқасы анықтамасының негізін құрайды, дəлірекайтқанда, олар қаржылық əрекеттердің жылдық орташатабыстылығын көрсетеді. Сонымен қатар, əрбір анықтамалардағы C1 капиталы A соманың (несие берілген соманың мөлшері) рөлінойнаса, ал C2 капитал C сомасына (қарызгердің қайтаратынсомасының мөлшері) сəйкес іс–əрекеттер жасай алады. 5.4. А н ы қ т а м а. (Қарапайым пайыздық үстема негізіндессуда беру схемасы – қаржылық əрекеттердің анологиясы).Қаржылық əрекеттердің табыстылығы (орташа жылдықтабыстылық) d1 деп үлес бірлігімен өрнектелген мына сандыайтады:
ал қаржылық əрекеттердің табыстылығы (орташа жылдықтабыстылық) D1 деп пайызбен өрнектелген мына санды айтады: D1 = 100 d1 (%). 22.5. А н ы қ т а м а. (Күрделі пайыздық үстеме негізінде ссудт беру схемасы жөнінде қаржылық əрекеттердің анологиясы).Қаржылық əрекеттердің табыстылығы (орташа жылдықтабыстылық) d 2 деп үлес бірлігімен өрнектелген мына сандыайтады:
ал қаржылық əрекеттердің табыстылығы (орташа жылдықтабыстылық) D2 деп пайызбен өрнектелген мына санды айтады: D2 = 100 d2 (%). 5.6. А н ы қ т а м а. (Үздіксіз пайыздық үстеме негізінде ссудаберу схемасы жөнінде қаржылық əрекеттердің анологиясы). Қаржылық əрекеттердің табыстылығы (орташа жылдықтабыстылық) d 3 деп үлес бірлігімен өрнектелген мына сандыайтады:
ал қаржылық əрекеттердің табыстылығы (орташа жылдықтабыстылық) D3 деп пайызбен өрнектелген мына санды айтады: D3 = 100 d 3 (%). Табыстылық d1 көп таралған көрсеткіш. Қаржылықəрекеттердің t2 – t1 ұзақтығы 1 жылдан əжептуір көп болғанжағдайда d2 табыстылығы қолданылады. Теориялық зерттеулердеміндетті түрде d 3 табыстылығы пайдалынылады. Мысалға, есептік пайыздық үстема негізінде ссуда берусхемасы жөнінде қаржылық əрекеттердің анологиясын қарастыруарқылы табыстылықтың басқа да нұсқасын зерделеуге болады. 5.1. Жылдық 12 % пайыздық үстемемен қарапайым пайыздарсхемасы бойынша 240 күнге фирмаға несие берілген. Несие бергенкезде несие берілген сома есебінен 1 % мөлшерде комиссиондықшығындар ұсталынған. Несие беруші үшін, бір жылда 360 күн депесептеп, қаржылық əрекеттің табыстылығын D 1 анықтаңыз. Несиеберуші үшін бір пайызға ұсталған комиссиондық шығындарқаржылық əрекеттердің табыстылығын қанша пайызға көтереді? Шешуі. Қаржылық əрекеттердің t2 – t1 ұзақтығы:
Сонымен, қаржылық əрекеттің табыстылығы: D1 = 13,64%. Сондықтан, несие берген кезде несиеге берілген соманыңесебінен 1% мөлшерде ұсталған комиссиондық шығындартабыстылықты 13,64 – 12 = 1,64 % жоғарылатады. Жауабы. Қаржылық əрекеттің табыстылығы D1 = 13,64 %. Бір пайызға ұсталған комиссиондық шығындар қаржылық əрекеттердің табыстылығын 1,64% жоғарылатады. 5.2. Жылдық 10 % үстемемен күрделі пайыздар схемасыбойынша 3 жыл мерзіміне фирмаға несие берілген. Несие бергенкезде несиеге берген сома есебінен 0,8% мөлшеріндекомиссиондық шығындар ұсталынған. Несие беруші үшінқаржылық əрекеттің табыстылығын D 2 анықтаңыз. Несие берушіүшін бір пайыз ұсталған комиссиондық шығындар қаржылықəрекеттердің табыстылығын қанша пайызға көтереді? Шешуі. Қаржылық əрекеттердің t2 – t1 ұзақтығы:
Осыдан кейін, (22.5) формуланы қолданып, Сонымен, қаржылық əрекеттің табыстылығы: D2 = 10,29%. Сондықтан, несие берген кезде несиеге берілген соманыңесебінен 1% мөлшерінде ұсталған комиссиондық шығындартабыстылықты 10,29 – 10 = 0,29% жоғарылатады. Жауабы. Қаржылық əрекеттің табыстылығы D 1= 10,29%. Бір пайызұсталған комиссиондық шығындар қаржылық əрекеттердің табыстылығын0,29% жоғарылатады. 5.3. Жылдық 15 % пайыздық үстемемен қарапайым пайыздарсхемасы бойынша 500 000 доллар вексельді банк 3 ай бойы өтеумезгіліне дейін есепке алады. Бір жылда 12 ай 30 күннен депесептеп, банк үшін осы қаржылық əрекеттің табыстылығын D1 анықтаңыз. Шешуі. Есептің шарты бойынша C = 500 000, e = 0,15 жəне t = 3 / 12=0,25. Бірінші кезекте (20.2) формуламен вексельдіңдисконтталған құнын табамыз: A = C – Cet = 500 000 – 500 000 · 0,15 ·0,25 = 481 250. Осыдан кейін, (22.4) формуланы қолданып,
Сонымен, қаржылық əрекеттің табыстылығы: D1 = 15,58%. Жауабы. Қаржылық əрекеттің табыстылығы D1 = 15,58%. Қаржылық əрекеттің қолма–қол табыстылығы. Қаржылық əрекеттің барлық ұзақтық [ t1, t2 ] аралығы үшінемес, сол уақыт аралығына жататын басқа да кез–келген уақытаралығына d1, d2, d3 табыстылықтарды есептеуге болады. Осыаралық ұзындығы нөлге дейін кемісе, əрбір d1, d2 жəне d3 табыстылықтардың шекті мəндерін есептегенде пайдалы. Мұндайшектеулікке өту қаржылық əрекеттердің қолма–қол табыстылығы түсінігіне алып келеді. Бір t уақыт мезгіліндегі қаржылық əрекеттердің қолма–қолтабыстылығын табу үшін, уақыт [t, t + D t ]аралығынқарастырайық жəне оның D t ұзындығын нөлге ұмтылдырайық.Осыдан, d 1 табыстылықтыаламыз:
формуладағы болғандықтан (5.8) өрнек C (t)–функциясының логарифмдіктуындысы деп аталады.Мына d2 – табыстылығы қарастырылған жағдайда:
С а л д а р. Бір t уақыт мезгіліндегі қаржылық əрекеттердіңқолма–қол d1 жəне d3 табыстылықтары C (t) – функциясыныңлогарифмдік туындысына тең. Мына d2 – табыстылыққарастырылған жағдайда, t уақыт мезгіліндегі қаржылықəрекеттердің қолма–қол табыстылығы алынған C (t) – капитал функциясыныңлогарифмдіктуындысыныңекспоненті 1(бірге) тең. 5.4. Уақытбойыншакапиталданлогарифмдіктуындысы f (t) –функцияғатең. Бір t = 0 уақытмезгіліндекапитал C0 ақшабірлігінқұрайды. Капиталдыңуақытбойынша C (t) өрнегінтабыңыз. Шешуі. (5.8) формуланықолданыптабамыз:
Жауабы. Капитал уақытпен байланысы (23.5) формуламенөрнектелінеді. С а л д а р. Уақыт бойынша капиталдың логарифмдіктуындысы тұрақты жəне k тең жағдайда (5.11) формуладанмынадай қатынас шығады: 12 ТАҚЫРЫП. ҚАРЖЫЛЫҚ-ЭКОНОМИКАЛЫҚЕСЕПТЕУЛЕРДЕГІ ƏДІСТЕРЖƏНЕМОДЕЛЬДЕР. Қаржылық немесе коммерциялық əрекеттердің ең қолайлысынтаңдау үшін оларға салыстыру жүргізіледі. Іс-əрекетке қатысушықұқықтық немесе физикалық тұлғалар олардың нəтижесін толықбілуге, пайдасын бағалай алуға, табыстылығын немесе нəтижеліктиімділігін анықтай алатындай болуға тиісті. Сондықтан,қарастырылатын тақырып – тəжірибеде маңызды жəне қаржыəрекеттеріндегі өзекті мəселелердің бірі. Қаржылық əрекеттердің қарапайым түрлерінің бірі ретінде,несиеге беруші A соманы қарызгерге n жылға беріп, одан осымерзімнің соңында C соманы қайтарып алатын жағдайды айтуғаболады. Мұндай əрекеттердің нəтижелік тиімділігін бағалау үшінтөмендегідей көрсеткіштер қолданылады: · қызығушылық деп аталатын, қатынастық өсу, кəдімгіпайыздық үстеме (қатынастық шама):
Қарастырылып отырған көрсеткіш несиеге берушініңкапиталының ұлғаюын сипаттайды жəне есеп кейде ұлғайту үрдісіделінеді. · бағасын кеміту қатынастығы немесе дисконт немесекəдімгі есептік үстеме:
Біресе алғашқы сома есебіне (қызығушылық), біресе соңғысома (дисконт) есебіне жатқызылатын осы көрсеткіштер несиегеберушінің капиталының ұлғаюын немесе кемуін сипаттайды жəнеолардың арасында мəнді байланыстар бар. Көрсетілген екі теңдіктібірге шешу арқылы келесі модельдерді алуға болады.
Қаржылық əрекеттерде кейде дисконттың орнына мынадайформуламен анықталынатын дисконт фактор қолданылады:
Қарапайым немесе күрделі пайыздардың эквиваленттікпайыздық үстемелер түсінігіне əкелетін, əртүрлі нұсқадағықаржылық нəтижелер тең деген жорамалдың негізінде, қаржылықəрекеттердің қолайлылығын анықтау үшін табыстар(табыстылықтар) салыстырылады. Эквиваленттік үстемелер (э -индексі барлық үстемелерсимволдарына жалғанады) бірдей қаржылық нəтижелерді немесеəртүрлі уақыт аралығында ұлғайтылған соманы көрсетеді. Сонымен, нақтылы пайыздық үстемелермен алғашқы соманың ұлғаюын есептеу мақсатында төмендегі базалық модельдерқолданылады.
Формулалардабіріншіреткездесетін p c, e c, p k, n жəне m символдары, сəйкесінше: p c– күрделіпайыздардыңжылдықүстемесі, қатынастықшама; e c – күрделіесептікпайыздардыңжылдықүстемесі, қатынастықшама; p k – номиналды (көрсетілген)жылдықпайыздықүстеме; n – келісіммерзімі, жылдар; m – біржылдағыесептеуаралықтарсаны. Қарастырылыпотырғанбазалықмодельдернегізіндеэквиваленттікүстемебайланыстарыныңбірнешемодельдерініңнұсқауларынжазуғаболады. Эквиваленттікүстемелердітабуүшін, келесіережебойыншаэквиваленттіктеңдеулерқұрайық. A капиталды n мерзімгеинвестрлеунəтижесінқарастырайық: C = A + T, мұндағыT – табыс (B – пайыздықақшаменсəйкес). Бұл əрекетті, оғанэквивалентті əрекет, мысалға, қарапайымпайыздарүстемесімен p қаражаттыіскесалу əрекетіменсалыстырайық. Білеміз, мұндайжағдайдаіскесалғанқаражатнəтижесі: C = A(1+p·n). Бұл іске салған қаражаттан алатын табыс: Сондықтан, қарапайым пайыздардың эквиваленттік үстемесі:
Ақшалар міндеттемесін есепке алсақ, мысалға, есептікүстемемен есептелген вексельдерде, табыс (дисконт) мына формулабойынша анықталынады: T = n ·e·C = C - A, Одан қарапайым пайыздардың эквиваленттік үстемесі теңболады:
Жоғарыда келтірген қарапайым пайыздардың екіэквиваленттік үстемесінің өрнектері негізінде басқа да үстемепайыздарының əртүрлі байланыс нұсқаларына эквиваленттіктеңдеулерді құруға болады. Мысалы, қарапайым жəне күрделіпайыздар схемасы бойынша есептеп қосып ұлғайтылған сомалардытеңестірсек: C = A(1+np); C = A(1+pэ)п мынадайэквиваленттітеңдеуаламыз: A(1+np) = A(1+pэ)п ,осыданқарапайымпайыздардыңэквиваленттікүстемесінанықтаймыз:
немесекүрделіпайыздардыңэквиваленттікүстемесін:
Күрделіпайыздардыесептепқосуүшінтөмендегідейэквиваленттіктеңдеуқұруғаболады:
одан pcэ - жылдықкүрделіпайыздардыңэквиваленттікүстемесін:
Сонымен, номиналды (көрсетілген) күрделіпайыздарүстемесінеэквиваленттіжəнеқаржылық əрекеттердің n мерзімменбайланыссыз, нəтижелікпайдалыжылдықкүрделіпайыздардың эквиваленттікүстемесі депаталатынкөрсеткіштіалдық. Нəтижелікпайдалыкүрделіпайыздарүстемесі, күрделі есептікүстемемен (ec) эквиваленттіжəнетең: соныменқатар, олэквиваленттіккүрделіноминалды (көрсетілген) есептікпайыздарүстемеменде (ek) сипатталады, яғни:
Сонымен, жоғарыда қарастырылған көрсеткіштер қаржылықəрекеттердің нақтылы табыстарын бағалау үшін немесе əртүрліпайыздық үстемелерді салыстыру үшін қажет. Нəтижесіндекапиталды инвестрлеу үшін дəйекті түрде пайдалы нұсқанытаңдауда, осы көрсеткіштер арқылы дұрыс шешімдер қабылданады. 6.1. 60 % – күрделі номиналдық (көрсетілген) пайыздарүстемесімен 2 жылға несие берілген. Квартал (тоқсан) сайынесептепқосуөткізіледі. Қарапайымжəнекүрделіпайыздықэквиваленттікүстемелерарқылықаржылық əрекеттіңнəтижеліктиімділігінбағалаңыз. Шешуі. Есептіңшартыбойыншабелгілі: pk = 0,6; n = 2; m = 4. а) Қарапайымпайыздардыңэквиваленттікүстемесі:
б) Күрделі пайыздардың эквиваленттік нəтижелік тиімді үстемесі:
Дисконттау əрекеттерінің модельдері. Дисконттау қаржы əрекеттерінде уақытқа байланыстыболатын өзгерістерді ескеруге мүмкіндік туғызады. Келешеккеқатысты көрсеткіштің бағасын, қазіргі уақыт мезгіліне келтіру əрекеті дисконттау деп аталатыны белгілі. Қарастырылып отырғанəрекет ұлғайту əрекетіне кері əрекет, яғни C шамасы бойынша A анықталынады. Мұндай жағдайда, C дисконтталынады немесеескеріледі делінеді, пайызды есептеп қосу жəне оларды ұстап қалуүрдісі – есептеу, ал ұсталынған пайыздар – дисконт деп театалады. Дисконттау арқылы табылған A шамасын, қазіргі капитализацияланған баға деп те атайды.Пайыздық үстемелерге байланысты екі түрлі дисконттау қолданылады: · математикалық дисконттау; · банктік (коммерциялық) санақ. 1. Математикалық дисконттау. Дисконттаудың бұл түрібасқа бір уақыт мезгілінде берілген C мəніне сəйкес келетін, біруақыт мезгіліндегі «қазіргі» немесе «келтірілген» деп аталатын A мəнін анықтауға байланысты. Бұл жағдайда (kd) дисконттықкоэффициент жəне (D) дисконт есептелінеді:
мұнда kd – дисконттық коэффициент (келтірілген), ол қарапайым пайыздар үстемесі бойынша:
Егер C сомасы күрделі пайыздар үстемесі бойынша есептелгенболса, онда дисконттау қазіргі уақыт мезгіліндегі баға:
мұнда kdс – дисконттық коэффициент (келтірілген), ол күрделі пайыздар үстемесі бойынша:
Егер C сомасы p k – номиналды (көрсетілген) жылдықпайыздық үстемесі бойынша есептелген жəне m – бір жылдағыесептеу аралықтар саны белгілі болса, онда:
Барлық жағдайларда мына формуламен дисконт анықталынады: D= C –A. 2. Банктік (коммерциялық) санақ. Дисконттаудың бұл түрініңмəнісі ақшалық міндеттемелерді сатып алумен түсіндіріледі. Мысалға, банк көрсетілген номинальдық бағасынан кіші бағағавексель сатып алу əрекетін жатқызуға болады. Мұндай жағдайда,вексель есепке алынды жəне клиент мына соманы алады, делінеді: A = C – D, мұндағы C – қарастырылып отырған міндеттеменің номиналдықсомасы; A – банк сатып алған вексельдің құны; D – пайыздықақшалардыңсомасы (банк табысы), дисконт. Вексельді сатып алушының пайыздық табысы жылдыққарапайым есептік үстеме арқылы анықталынуы мүмкін:
Егер есепке алынған күннен өтеу күніне дейінгі мерзім n біржылға толмайтын болса, онда дисконт мына формуламенанықталады:
13 ТАҚЫРЫП. ОБЛИГАЦИЯЛАРМЕНҚАРЖЫЛЫҚ ƏРЕКЕТТЕРДІҢМОДЕЛЬДЕРІ. Облигация дегеніміз қарызы үшін сенімділікке берілген құндықағаз, яғни онымен қарызгер несие берушіге келісілген мерзімібіткеннен кейінгі келешектегі күндегі пайызымен қоса, тиістітолық соманы төлейтіні туралы кепілдік береді. Облигацияны эмитент шығарады, онда оның номиналдыбағасы жəне қанша мерзімге шыққаны туралы мəліметтеркөрсетіледі. Мерзімі біткеннен кейін эмитент номиналдыбағасымен сатып алады (өтеледі), яғни қайтарып алынады. Облигацияны номиналынан кіші бағамен сатып алып, осыісімен сатып алушы эмитетке ссуда береді де, ал ол тəжірибеденесие берушіге айналады. Мұндай жағдайда сатып алушы (несиегеберуші), номинал мен сатып алған құнның айырымыменанықталатын табыс алады, оны дисконт деп атайды. Егероблигациямен бірге купон берілсе, ондағы көрсетілген үстемебойынша, мысалға, жыл сайын немесе квартал сайын пайыздықүстемелер төленеді. Бұл купондық табыс деп аталатын қосымшатабыс. Облигациялар мен əрекеттердің мақсаты – табыс табу үшінқаражатты іске салу нұсқаларының біреуін тəжірибеде қолдану,сөйтіп капиталды құнсызданудан қорғауды қамтамасыздандырадыжəне инфляция жағдайында оның өсуіне кепілдік беріледі.Облигацияны сатып алу табыстылығын есептеуденоминалдың пайызымен өрнектелген облигацияның құнымен анықталатын курс туралы түсінік қолданылады:
мұндағы A - облигация құны; H - облигацияның номиналдық бағасы; A k- облигация курсы. Осыдан, облигацияның курсы белгілі болса, онда оның құны:
Егер облигациялар бойынша пайыздар төленсе, онда оларды пайыздылықтар деп атайды, ал əрбір төлемнен табыс олардыңноминалдық бағалары бойынша есептелінеді:
Егер облигациялар бойынша пайыздар төленбейтін болса,онда сатуға ұсынған құнмен (номинал, эмитент) сатып алынғанқұнның айырымы табыс көзі болып есептелінеді, бұл айырымдыдисконт деп атайды, ал мұндай облигациялар диконттықтар депаталады, мысалға мемлекеттік қысқа мерзімдік міндеттемелер(МҚММ). Мұндай облигациялардың табысын номиналдан сатыпалған бағаны алып тастау арқылы есептейді:
Өтелетіноблигациялардыңтабыстылығынқарапайымпайыздардыңэквиваленттікүстемесібойыншаанықтауғаболады:
Ұзақмерзімдікоблигацияларпайыздарыныңтөлеміменқосасатыпалғаннантүсетінтабыс – олардыөтеу (номиналь) құннансатыпалғанқұнныңайырымыжəнепайыздарсомасықосындыларынантұрады. Егероблигацияларбойыншапайыздаржылдыңсоңындатөленетінболса, мысалы, күрделіпайыздарүстемесі pc бойыншапайыздықақшаларсомасыоблигацияларды n жылданкейінөтегендемынаөрнекпенанықталынады:
Жалпытабыстымынаформулабойыншаанықтаймыз:
Облигациянысатыпалу-өтеу əрекеттерініңтабыстылығынкүрделіпайыздардыңнəтижелітиімдіүстемесітүріндемынаөрнекпенанықтауғаболады:
Келтірілгенқатынастардыңнегізіндемыналардыаламыз:
Егерпайыздаркезең-кезеңіментөленетінболса, ондажалпытабыстыанықтағандареинвестрлеумүмкіндігінескергенжөн. 6.15. Облигацияның номиналдық бағасы 5000 теңге, ал курсы75 –ті құрайды. Облигацияның құнын анықтаңыз. Шешуі. Ak =75; H =5000 теңге. Облигацияның құны:
Акциялармен қаржылық əрекеттердің модельдері. Акция дегеніміз, дивидент алуды қамтамасыз ететін жəнеакция ұстаушының нақтылы меншігінің үлесін көрсететін, құндықағаздардың бір үлес бөлігі. Дивидентті есептеп қосу жəне төлеуретіне байланысты акцияны кəдімгідей жəне ерекшеленгендер депбөледі. Ерекшеленген акция бойынша дивиденд оның номиналдық бағасының H бекітілген пайыздарымен алынады деп алдыналахабарландырылады жəне ол мына өрнек арқылы анықталады: Дв = рдж ·H,мұндағы рдж – дивидендтің жылдық үстемесі. Бір кəдімгідей акциядан алынатын табыс:
мұнда Мк – кəдімгідей акциялардың саны; ТП – бөлінетін таза пайда; Дер – барлық ерекшеленген акциялардың девиденті, Дер = Мер·Дв; Мер – ерекшеленген акциялардың саны. Жалпы кəдімгідей акциялар бойынша дивиденттерді төлеуүшін барлық табыстар түгелімен берілмейді, тек оның бір бөлігіжұмсалады. Сондықтан дивиденд үшін төленген шамадивиндендтік шығынмен Дшыг анықталады:
Акциялар бойынша табыстылық төленетін дивидендтердентүсетін табыспен анықталынады, сонымен қатар инвестицияныңнəтижелік тиімділігін анықтайтын, акцияның сатып алынған құнымен оны сатып жібергендегі құнның айырымы:
мұнда Аа – сатып алғандағы акцияның құны; Аж – сатып жібергендегі акцияның құны; Д – акция меншікті болған кездегі дивиденд. Акциялармен жасалған əрекеттерге талдау жүргізу үшінбірнеше көрсеткіштер бойынша есептеулер жүргізу керек. Ағымдағы табыстылық, салық салымынсыз мына формула бойынша анықталады:
мұнда Аа – сатып алынған құн немесе акцияның курстық бағасы. Акцияның курстық бағасы банктік депозиттік үстемесімен p салыстыру арқылы анықталады:
Ақырғы табыстылық дивидендтердің қосындыларымен жəнеқайта сату арқылы қосымша түскен табыстар бойыншаанықталады: Ағымдағы табыстылық, салық салымын есепке алып, мынаөрнекпен анықталады:
Жоғарыдағы келтірілген формуладан басқа да формуламенакцияның курстық бағасын анықтауға болады, мысалы, оныңноминалдық құны арқылы:
Акцияның нарықтық құны оның сұранысына байланыстыанықталады, демек, акцияның нарықтағы құндылық көрсеткішітабылады:
Акциялармен ұзақ мерзімдік əрекеттер жүргізілген кездердеэквиваленттік үстемелерді анықтайтын қарапайым жəне күрделіпайыздар формулаларын қолдануға болады: C = A (1 + n·pэ); C = A (1 + pэ) n. Мұндайжағдайдақаржылық əрекеттердіңтабысымынаформулаларменанықталады: T = C-A = A·n·pэ; T = A [(1+ pэ) n – 1], оданқарапайымжəнекүрделіпайыздардыңэквиваленттікүстемелері:
Сонымен, жоғарыдағы келтірілген модельдерді қолданып,акциялармен жүргізілетін қаржылық əрекеттердің тиімділігінсалыстыру арқылы оптималды инвестрлік жобаларды таңдаумəселелерін шешуге болады. 6.24. Өткен жылғы акциялар бойынша жай қалыптағы жылдықдивидендтері 20 %, ал ерекшеленгендерінің жылдық дивидентері30 % құрайтыны туралы банк хабарландыру жасады. Номиналы30000 теңге ерекшеленген акцияның жəне номиналы 10000 теңгекəдімгідей акцияның біреуінің дивидендтер сомасын анықтаңыз. Шешуі. Бір ерекшеленген акцияның дивидендтер сомасы тең: Д ер = 0,3 · 30 000 = 9 000 теңге. Бір жай қалыптағы акцияның дивидендтер сомасы тең: Д к = 0,2 · 10 000 = 2 000 теңге. 6.25. Егер акция 5 жылдан кейін сатылатын болса, жыл сайын20% мөлшерде жылдық дивиденд алынса жəне жыл сайынғыбағаның өсімі номинал(дың 10 % құрайтын болса, онда номиналы10000 теңге тұратын акцияны сатып алғаннан қанша табыстүсетінін күтуге болатынын жəне əрекеттердің табыстылығынанықтаңыз. Шешуі. Н =10000 теңге; рдж = 0,2; n =5 жыл; D A 1= 0,1 H. 5 жылда жылдық дивиденд шамасы құрайды:
5 жылдан кейін акция бағасы тең:
Жалпы табыс құрайды: Та = Д + Аа – Н = 10000 + 15000 – 10000 = 15000 теңге. Күрделі пайыздардың эквиваленттік үстемесі түрінде акцияны сатып алудың табыстылығы құрайды:
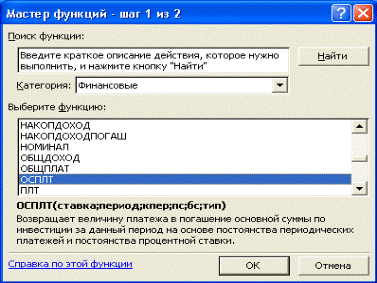
14 ТАҚЫРЫП. MSEXCEL-ДЕҚАРЖЫЛЫҚЕСЕПТЕУЛЕР. Əртүрлі қаржылық есептеулер жүргізуге арналған MS Excelқұрлымына бірнеше функциялар отырғызылған мысалға, пайыз бойынша төлемді табу, займ бойынша кезегінде өтелетін ақша мөлшерін есептеу, салынған капиталдың тиімділігін анықтау жəне т.б.с.с.). Сондықтан əртүрлі қаржылық талдауларды компьютер көмегімен жүргізгенде осы қаржылық функцияларды MS Excel-де қолдану əдістерін білген ауадай қажет. MS Excel-де экономикалық есептеулер жүргізу үшін мынадайқұралдар қолданылады: · MS Excel-де қаржылық функция; · параметрлерді таңдап алу; · орын-орынына қою кестелері; · сценарилар диспетчері. Қаржылық функциялардың толық тізімін (егер олқарастырымаса) шығару үшін, MS Excel 2000 жəне одан жоғарыверсияларында Пакет анализа Сервис → Надстройка →список Настройки) флажок қою ұсынылады. MS Excel-дің қаржылық функциялары. MS Excel-дің қаржылық функциялары, күрделі есептеулержүргізуге қажетті, базалық шамаларды есептеуге арналған.Олардың аттарының белгілері бірнеше рет өзгерді жəне MS Excel2000 жəне одан жоғары версияларында кейінгі кездердеқолданылатын олардың белгілері орыс тілінде жазылған оқуқұралдарында [] кеңінен толық беріледі. MS Excel-дің қаржылық функцияларын қолдану үшінмынадай іс-əрекеттер жүргізіледі: 1. Функцияның негізгі аргументтерінің мəндерін жұмысшыбетте арнайы ұяларға енгізіңіз 2. MS Excel құрлымында отырғызылған қаржылықфункцияны қолдану арқылы, формула енгізілетін ұяға өтіңіз. 3. Вставка → Функция →категория Финансовые бұйрығыарқылы мастер функцияларды шақырыңыз да (7.1-сурет),функциялар тізімінен өзіңізге керекті қаржылық функциянытаңдаңыз (7.1-сурет). 7.1-сурет. Мастер функция терезесінде қаржылық функцияларды таңдау
Кеңес. Сұхбаттасу терезесіндегі енгізу поляларына тиісті аргумент- тердің мəндері жазылған ұялар адресін немесе сондағы сан мəндерді енгізуге болады.
|



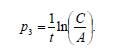







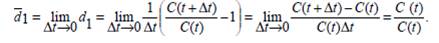
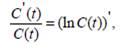


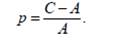


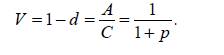
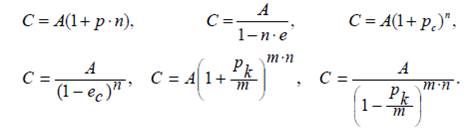

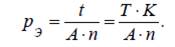
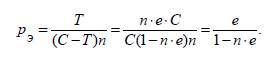


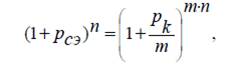
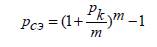 аламыз.
аламыз.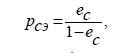






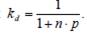


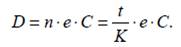


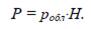 .
.



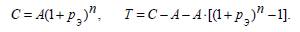
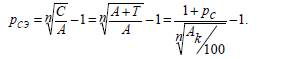
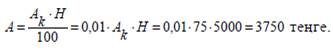

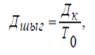 мұнда Дк – бір кəдімгідей акцияның дивиденті.
мұнда Дк – бір кəдімгідей акцияның дивиденті.
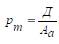

 мұнда рсс – салық салым үстемесі.
мұнда рсс – салық салым үстемесі.
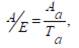 мұнда Та – акцияны нарықта сатқаннан түскен табыс.
мұнда Та – акцияны нарықта сатқаннан түскен табыс.