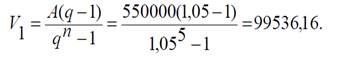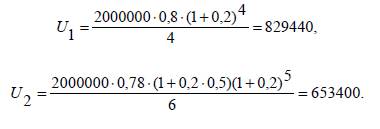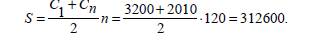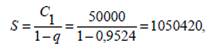БІРДЕЙ ТӨЛЕНЕТІН(ТҰТЫНУШЫЛАР НЕСИЕЛЕРІ) ССУДАЛАРДЫ ӨТЕУ
Алдыңғы қарастырылған тақырыптарда, қарызгер пайыздық ақшасымен қоса қарызын бір төлемен, несие беру келісімінде қойылған ерзім соңында, несие берушіге қайтару жағдайы келтірілген. Қарастырылып отырған тақырыпта, ссуданың қарызгерге бірден толық берілетіні, ал оны қайтару (өтеу), төлеу өлшерлері бірдей немесе арифметикалық немесе геометриялық прогрессия бойынша əртүрлі төлемен жүретін жағдайлары қарастырылады. Бір жағдайларда қарызгерге ссуданы өлшерлері бірдей төлемен өтеу пайдалы, өйткені ол қарыз ауыртпалығын ссуда берілген барлық ерзімге бірдей бөлуге үмкіншілік туғызады.Басқа жағдайларда, егер қаржыландырудың басында қаржының түсе бастаған бірінші күндерінде қарызды көп өлшерде қайтару мүмкін болмаса, онда қарызгерге ссуданы өлшерлері бірдей төлемен өтеу пайдалы болмайды. 6.1. А н ы қ т а м а. Тұтынушылық несие деп, қарыз соманы (пайыздық ақшасымен қоса) n рет бірдей өлшерде өтеу, бірдей уақыт аралығы өткен сайын жүргізілетін, p жылдық пайыздық үстемемен t (жыл) ерзімге берілген A өлшердегі ссуданы, сондай–ақ қарапайым пайыздар қарастырылған жағдайда əр өтеу төлем өлшері: Z= ал күрделі пайыздар қарастырылған жағдайда əр өтеу төлемінің мөлшері: Z= болған жағдайларды атайды. 6.2. А н ы қ т а м а. Уақыт аралығының бас кезінде өтейтін төлем - алдыңғы нумерандо (пренумерандо), соңында өтейтін төлем- соңғы нумерандо(постнумерандо) деп аталады. 6.1. Сатып алушы, бағасы 40500 теңге тұратын шаңсорғыш сатып алу үшін, банктен несиеге ақша сұрады. Банк сатып алушыға бір жылғы пайыздық үстемесі 12% негізінде қарапайым пайыздар схемасы бойынша есептесуге жəне ай сайын соңғы нумерандо (яғни айдың соңында) ен өтеуге1,5 жыл ерзіміне тұтынушылық несие берді. Сатып алушы ай сайын қандай соманы банкке аударуы керек? Шешуі. Мына көрсеткіштер n=18; p=0,12; t=1,5 жəне A=40500 белгілі болғандықтан, (6.1) формуланы қолданып, табамыз: Жауабы. Ай сайын сатып алушы банкке2655 теңге аударуы тиіс. 6.2. Сатып алушы бағасы 40 000 доллар тұратын жеңіл машина сатып алу үшін, банктен несиеге ақша сұрады. Банк сатып алушыға жылғы пайыздық үстемесі9% негізінде күрделі пайыздар схемасы бойынша есептеуге жəне ай сайын нумерандо мен өтеуге 3 жыл ерзіміне тұтынушылық несие берді. Сатып алушы ай сайын қандай соманы банкке аударуы керек? Z= Шешуі. Мына көрсеткіштер A = 40 000; n = 36; p = 0,09 жəне t = 3 белгілі болғандықтан, (11.2) формуланы қолданып, табамыз: Жауабы. Ай сайын сатып алушы банкке1438,889 доллар аударуы тиіс. Несие берушіге тұтынушылық несие өте қызықты болғанымен, ал қарызгерге қатысты бұл несие шектен тыс əділетсіз. Сөзсіз, ссуданы өтеу ерзімінің соңында бір төлемен қайтаратын жағдай сияқты, тұтынушылық несие жағдайында да несие беруші, сол пайыздық ақшаны қарызгерден алаалады. Бірақ, тұтынушылық несиенің ұндай ссудалардан өзгешелігі, несие берушіге қарызгер қарызын өтеуді ерте бастайды жəне несие берушіде алдын ала қайтарылған ақысыз ақшаны басқа іске қолдануына үмкіндік туады. Мысалға, басқа клиентке тұтынушылық несие бере алады. Нəтижесінде несие бергені үшін, қарызгер төлейтін пайыздық ақша сомасынан көп асатын төлемді несие беруші алаалады. Осы ойымызды төмендегі есептерді шығарып, дəлелдейік. Басында қарапайым пайыздар схемасымен есептейтін тұтынушылық несие жағдайын қарастырайық. 6.3. Несие берушінің көзқарасында, 6.1 мысалды қайта қарастырайық, яғни сатып алушы бағасы 40500 теңге тұратын шаңсорғыш сатып алу үшін, банктен несиеге ақша сұрады. Банксатып алушыға жылғы пайыздық үстемесі 12 % негізінде қарапайым пайыздар схемасы бойынша есептесуге жəне ай сайын соңғы нумерандоен өтеуге1,5 жыл ерзіміне тұтынушылық несие берді. Сатып алушы ай сайын қандай соманы банкке аударуы керек? Шешуі. Əр ай сайын қарызгердің соңғы төлем езгіліне дейін (18–ші айдың соңы), несие беруші 17 ай бойы айдың соңында төленетін 2655 теңгені пайдаланып келді. 12 % қарапайым пайыздық үстеме бойынша 1–ші айдың соңында төлеген 2655 теңгені (4.30) формуламен анықтасақ ол 18–ші айдың соңында мынадай сомамен эквивалентті: 2665*(1+0,12 Сонымен қатар несие беруші 16 ай бойы, 2–ші айдың соңында төленетін 2655 тенгені пайдаланады. 12% қарапайым пайыздық үстеме бойынша 2–ші айдың соңында төлеген 2655 теңгені (4.30) формуламен анықтасақ ол 18–ші айдың соңында мынадай сомамен эквивалентті: 2665*(1+0,12 Осылай талқылай келе 3–ші айдағы төлем ынадай сомамен эквивалентті: 2665*(1+0,12
жəне т.б. Ең ақырғы 18–ші айдың соңында 2655 теңгені қарызгер қайтарады. Сөйтіп, 18 үшелі кемімелі арифметикалық прогрессия {аn} алынды. a1=3106,08; a2=3079,53; a3=3052,98; …, a18 =2655,00, айырымы d тең: d = 2665*(1+0,12 Енді осы арифметикалық прогрессияның қосындысын есептейік: a1+a2+a3+…+a18 = Осыдан барып, «шындығында» несие үшін: 51849,72 – 40500 = 11349,72 теңге төленгенін анықтаймыз. Алынған нəтижені салыстыру үшін, қарастырылып отырған ысалдың əліметтері бойынша пайыздық ақша өлшерін анықтайық: B = Apt =40500*0.12* Сонымен, «шындығында» несие беруші несиелік келісімде көрсеткен сомадан 11349,72 – 7290 = 4059,72 теңге көп алады. Жауабы. «Шындығында» несие беруші несиелік келісімде көрсеткен сомадан4059,72 теңгені артық алады Тұтыну несиесі күрделі пайыздар схемасымен есептелінетін жағдайға өтейік. Пайыздық ақшалары қосылған ссудаларды бірдей төлемдермен өтеу. Қарастырылып отырған тақырып, алдыңғы тақырыптағы сияқты, бірдей төлемдер арқылы, əртүрлі уақыт кезеңдерінде іске асырылатын, ссудаларды өтеу əдістері баяндалады. Алдыңғы тақырыпқа қарағанда тақырыптың өзгешелігі, қарызгерге қатысты біршама пайдалы іс жасалады, яғни əр кезеңде тиісті төлемдерді өтеуде оларға есептелген пайыздық ақшалары да ссудаларды өтеу есебіне кіргізіледі. 6.3. А н ы қ т а м а. Аннуитеттер деп - жыл сайын іске асырылатын төлемдерді атайды. 6.5. Жылдық пайыздық үстемесі 10 % негізінде қарапайым пайыздар схемасы бойынша есептеліп, 5 жыл ерзімге займға (қарызға) берілген350 000 доллар бірдей постнумерандо(жылдың соңында) аннуитеттермен өтеледі. Несие беруші осындай схема бойынша, əр аннуитетті алған езгілден займның біткен мерзіміне дейін оны пайдаланғаны үшін, пайыздық ақшаларын есептеп, займды өтеу есебіне кіргізеді. Аннуитеттердің əндерін табу керек. Шешуі. Есептің шарты бойынша ына көрсеткіштер n = t = 5; p = 0,1 жəне A=350 000 белгілі. Есепті шығару үшін біріншіден, n, p, A кез келген əндерінде аннуитеттердің U əнін табуға мүмкіндік беретін формуланы анықтау қажет. Содан кейін табылған формулаға есептің шарты бойынша берілген көрсеткіштердің əндерін енгіземіз. Несие беруші бірінші аннуитетпен(n–1) жылдар бойы, екінші аннуитетпен (n–2) жылдар бойы жəне т.б. жылдар бойы пайдаланатынына байланысты пайыздық ақшаларды есептеу үшін қарапайым пайыздар C=A(1+pt) формуласын пайдаланып, төмендегідей теңдеу құрамыз: U(1 + (n – 1)p) + U(1 + (n– 2)p) + … + U= A(1 + np). (6.3) (6.3) теңдеуденаннуитеттіесептейтінформуланыаламыз: U = Арифметикалықпрогрессияүшелерініңқосындысыформуласыныңкөмегімен, (6.4) формуланыңбөлімінмынатүрдежазaмыз:
Нəтижесінде(3.4) формуланыынадайтүргекелтіреміз: U= (6.5) формулағаесептегікөрсеткіштердің əндеріненгізіп, аннуитеттіесептейміз U= Пайыздықақшаларесептелмегенжағдайдағыаннуитетті(6.1) формулабойыншаесептеп, (3.6) формуламентабылғананнуитетпенсалыстырамыз. U= Сөйтіп, қарызгерүшін (6.6) формуламенесептеп, өтелген 87 500 доллартөлемөлшері, (6.7) формуламенесептелген 105 000 доллартөлемөлшерінеқарағандакөпарзанжəнетиімді. Жауабы. Аннуитет 87500 долларғатең.
7 ТАҚЫРЫП. ҚАРЫЗҚАЛДЫҒЫНАБАЙЛАНЫСТЫПАЙЫЗДЫҚАҚШАЛАРЫЕСЕПТЕЛІНЕТІН, БІРДЕЙТӨЛЕМДЕРМЕНССУДАЛАРДЫӨТЕУ. Төлемдердіөтеуүрдісін - қарыздыөтеугежауапберетінжəнепайыздықақшалардыөтейтіндепекітопқабөлу, принциптіктүрдемаңызды. Себебі, салықтөлеміосытоптарғабайланыстыанықталады. Қарастырылыпотырғантақырып, жылдықпайыздықүстемесімен p % қарапайым немесе күрделі пайыздарсхемасыбойыншаберілгенпайыздықақшалардыөтеугекететін əрбірөтеутөлемдерініңбөліктері, өтеутөлемінөткізгенмезгілдегіқарызқалдықтарының (пайыздықақшалардықоспағанда) p % тең, ссудалардыөтеу əдісінбаяндауғабағытталған. Осы əдістіалдыңғытақырыптағы 12.2 есебінемағынасынаұқсасесепкеқолданужолынқарастырайық. Есеп. Жылдықпайыздықүстемесі 6% негізінде күрделі пайыздарсхемасыбойыншаесептелінетін, 5 жылмерзімгезаемге (қарызға) берілген 550 000 доллар, бірдейпостнумерандо (жылсоңында) 130 568,02 доллараннуитетпенөтеледі. Пайыздықақшалардыөтеугекететін, əрбіраннуитеттіңбөліктері, өтеутөлемінөткізгенмезгілдегіқарызқалдықтарының (пайыздықақшалардықоспағанда) 6% құрайды. Заемдыөтеужоспарынқұрыңыз. Шешуі. Мынадайбелгілердіенгіземіз: B1, B2, B3, B4, B5 – 1, 2, 3, 4, 5–шіжылдардағы пайыздықтөлемдер, яғнисəйкесінше (пайыздықақшалардыөтеугекететінаннуитеттербөліктері); V1, V2, V3, V4, V5 – 1, 2, 3, 4, 5–шіжылдардағы қарызтөлемдері, яғнисəйкесінше (қарыздыөтеугекететін, аннуитеттербөліктері); O1, O2, O3, O4, O5 – аннуитеттердіенгізгенненкейінгі 1, 2, 3, 4, 5-шіжылдардағы қарызқалдықтары; Əржылдағыаннуитеттіңмөлшері U = 130 568,02 доллар. Сонымен, барлықпайыздықақшаларсомасы: B = B1 + B2 + B3 + B4 + B5. Қарызүшінтөленгенақшаларсомасынемесежалпықарызмөлшері: A = O = V1 + V2 + V3 + V4 + V5. Біріншіпайыздықтөленгенақшанытабайық: B 1 = 550 000 ·0,06 = 33 000. Қарыздыөтеуүшін 1–шіжылдағытөленгенақшамөлшері,аннуитетпенпайыздықтөлемайырымынантұрады, яғни: V1 = U – B1 = 130 568,02 – 33 000 = 97 568,02. Сондықтан, біріншітөлемненкейін, қарыз 97 568,02 долларғақысқарадыда: O1 = O – V1 = 550 000 – 97 568,02 = 452 431,98 долларқалады. Қалғанқарызмөлшерінен 2–шіжылыпайыздықтөленгенақшамөлшері: B 2 = 452 431,98 · 0,06 = 27 145,92. Қарыздыөтеуүшін 2–шіжылғытөленгенақшамөлшері(аннуитетпенпайыздықтөлемайырымы): V2 = U – B 2 = 130 568,02 – 27 145,92 = 103 422,11. Біріншіжылғыаннуитеттіенгізгенненкейінгі 2–шіжылғықарызқалдығы: O2 = O1 – V2 = 452 431,98 – 103 422,11 = 349 009,87. Əріқарайжоғарыдағыкелтірілгентəсілменмыналардыанықтаймыз: – 3–шіжылғы B3 = 349 009,87 · 0,06 = 20 940,59, V3 = U – B3 = 130 568,02 – 20 940,59 = 109 627,43, O3 = O2 – V3 = 349 009,87 – 109 627,43 = 239 382,44, – 4–шіжылғы B4 = 239 382,44 · 0,06 = 14 362,95, V4 = U – B 4 = 130 568,02 – 14 362,95 = 116 205,08, O4 = O3 – V4 = 239 382,44 – 116 205,08 = 123 177,36, – 5–шіжылғы B5 = 123 177,36 · 0,06 = 7 390,64, 3.1–кесте. Займды өтеу жоспары
V5 = U – B5 = 130 568,02 – 7 390,64 = 123 177,36. Егер 4–ші жылы қалған қарыздан ақырғы төлемді алып тастасақ, онда қарыздың толығымен төленгенін көреміз: O5 = O4 – V5 = 123 177,36 – 123 177,36 = 0. Жауабы. Зайымды өтеу жоспарын 3.1–кестемен келтірейік. 8 ТАҚЫРЫП. ҚАРЫЗҚАЛДЫҒЫНАБАЙЛАНЫСТЫПАЙЫЗДЫҚАҚШАЛАРЫӨТЕЛЕТІН, ГЕОМЕТРИЯЛЫҚПРОГРЕССИЯЗАҢДЫЛЫҒЫМЕНӨЗГЕРЕТІНТӨЛЕМДЕРМЕНССУДАЛАРДЫӨТЕУ. ЕСЕП. Заемгеберілген 550 000 долларпостнумерандоаннуитетімен 5 жылбойыөтеледі. Біржылданбіржылғаөткенсайынқарызтөлемі: а) 5 % өседі; б) 5 % кемиді. Жылдық күрделі пайыздықүстеме 10 %. Пайыздықақшаларжəнеаннуитеттересепкекірмейді. Əрбіркөрсетілгенжағдайғазаемдыөтеужоспарынқұрыңыз. Шешуі. Есептіңшартыбойыншамынакөрсеткіштер A =550 000 n = t = 5; p = 0,1 жəнеа) q = 100% + 5% =105% немесеүлесбойынша q = 1,05 (геометриялықпрогрессияныңбөлімі)белгілі. Барлыққарызтөлемі (заемгеберілгенақшасомасы) барлықгеометриялықпрогрессиямүшелерініңқосындысы. Геометриялықпрогрессиямүшелерініңқосындыныңформуласынқолданып,оныңбіріншімүшесінтабайық:
Алынған формуладағы V1 геометриялық прогрессияныңбіріншімүшесі, олқарыздықайтарудағыбіріншітөлеммөлшерінкөрсетеді, яғни:
1–шіжылдыңсоңындақалғанқарыз: O1 = A – V1 = 550 000 – 99 536,16 = 450 463,84. Біріншіпайыздықтөлем: B1 = 550 000 · 0,1 = 55 000. Біріншіаннуитет: U1 = V1 + B1 = 99 536,16 + 55 000 = 154 536,16. Екіншітөлем: V2 = qV2 = 1,05·99 536,16 = 104 512,96. 2–шіжылдыңсоңындақалғанқарыз: O2 = O1 – V2 = 450 463,84 – 104 512,96 = 345 950,88. Екіншіпайыздықтөлем: B2 = p·O1 = 0,1 · 450 463,84 = 45 046,38. Екіншіаннуитет: U2 = V2 + B2 = 104 512,96 + 45 046,38 = 149 559,34. Үшіншітөлем: V3 = qV2 = 1,05·104 512,96 = 109 738,6. 3–шіжылдыңсоңындақалғанқарыз: O3 = O2 – V3 = 345 950,88 – 109 738,6 = 236 212,28. Үшіншіпайыздықтөлем: B3 = p·O2 = 0,1 · 345 950,88 = 34 595,09. Үшіншіаннуитет: U3 = V3 + B3 = 109 738,6 + 34 595,09 = 144 333,69. Төртіншітөлем: V4 = qV3 = 1,05· 109 738,6 = 115 225,53. 4–шіжылдыңсоңындақалғанқарыз: O4 = O3 – V4 = 236 212,28 – 115 225,53 = 120 986,75. Төртіншіпайыздықтөлем: B4 = p·O3 = 0,1 · 236 212,28 = 23 621,23. Төртіншіаннуитет: U4 = V4 + B4 = 115 225,53 + 23 621,23 = 138 846,76. Бесіншітөлем: V5 = qV4 = 1,05 · 115 225,53 = 120 986,75. 5–шіжылдыңсоңындақалғанқарыз: O5 = O4 – V5 = 120 986,75 – 120 986,75 = 0,00. Бесіншіпайыздықтөлем: B5 = p·O4 = 0,1 · 120 986,75 = 12 098,68. Бесіншіаннуитет: U5 = V5 + B5 = 120 986,8 + 12 098,68 = 133 085,48. Есептелінгенкөрсеткіштерді 3.5–кестегежазып, а) жағдай- дағызаемдыөтеужоспарынқұрамыз. 3.5–кесте. а) жағдайында заемды өтеу жоспары
б) бұлжағдайдаа) жағдайғақарағандагеометриялықпрогрессияныңбөлімітең: q= 1–0,05= 0,95, осыданбірінші V1 төлеммөлшерінесептейміз:
1–шіжылдыңсоңындақалғанқарыз: O1 = A – V1 = 550 000 – 121 563,49 = 428 436,51. Біріншіпайыздықтөлем: B1 = 550 000 · 0,1 = 55 000. Біріншіаннуитет: U1 = V1 + B1 = 121 563,49 + 55 000 = 176 563,49. Екіншітөлем: V2 = qV1 = 0,95·121 563,49 = 115 485,43. 2–шіжылдыңсоңындақалғанқарыз: O2 = O1 – V2 = 428 436,51 – 115 485,43= 312 951,08. Екіншіпайыздықтөлем: B2 = p·O1 = 0,1 · 428 436,51 = 42 843,65. Екіншіаннуитет: U 2 = V2 + B2 = 115 485,43 + 42 843,65 = 158 329,08. Үшіншітөлем: V3 = qV2 = 0,95·115 485,43 = 109 711,16. 3–шіжылдыңсоңындақалғанқарыз: O3 = O2 – V3 = 312 951,08 – 109 711,16 = 203 239,92. Үшіншіпайыздықтөлем: B3 = p·O2 = 0,1 · 312 950,08 = 31 295,00. Үшіншіаннуитет: U3 = V3 + B3 = 109 711,16 + 31 295,00 = 141 006,16. Төртіншітөлем: V4 = qV3 = 0,95· 109 711,16 = 104 225,60. 4–шіжылдыңсоңындақалғанқарыз: O4 = O3 – V4 = 203 239,92 – 104 225,60 = 99 014,32. Төртіншіпайыздықтөлем: B4 = p·O3 = 0,1 · 203 239,92 = 20 323,99. Төртіншіаннуитет: U4 = V4 + B4 = 104 225,6 + 20 323,99 = 124 549,59. Бесіншітөлем: V5 = qV4 = 0,95 · 104 225,60 = 99 014,32. 5–шіжылдыңсоңындақалғанқарыз: O5 = O4 – V5 = 104 225,60 – 104 225,60 = 0,00. Бесіншіпайыздықтөлем: B5 = p·O4 = 0,1 · 120 986,75 = 12 098,68. Бесіншіаннуитет: U5 = V5 + B5 = 120 986,8 + 12 098,68 = 133 085,48. Есептелінгенкөрсеткіштерді 3.6–кестегежазып, б) жағдай- дағызаемдыөтеужоспарынтұрғызамыз. 3.6–кесте. б) жағдайында заемды өтеу жоспары
Жауабы. Есепте қарастырылып отырған жағдайлардағы заемды өтеу жоспарлары есептеу нəтижесінде, сəйкесінше 3.5 жəне 3.6–кестелерде құрылып, келтірілген. 3.11. Заемге берілген 550 000 доллар, соңғысы басқаларынанөзгеше, ал қалғаны заемның 35% құрайтын аннуитеттерменөтелмекші. Жылдық күрделі пайыздық үстеме 10 %. Пайыздықақшалар жəне аннуитеттер есепке кірмейді. Заемды өтеу жоспарынқұрып, соңғы аннуитетті анықтаңыз. Шешуі. Соңғы барлық аннуитеттердің мөлшерін есептейік: U = 550 000 · 0,35 = 192 500. Қарыздың бірінші төлемі жəне бірінші пайыздық төлем бірінші аннуитетті құрайды. Бірінші пайыздық төлем: B 1= 550 000 · 0,1 = 55 000. Қарыздың бірінші төлемі: V1 = U – B 1 = 192 500 – 55 000 = 137 500. Бірінші төлемнен кейін қалған қарыз: O1 = A – V1 = 550 000 – 137 500 = 412 500. Екінші пайыздық төлем: B2 = p·O 1 = 0,1 · 412 500 = 41 250. Қарыздың екінші төлемі: V2 = U – B 2 = 192 500 – 41 250 = 151 250. Екінші төлемнен кейінгі қалған қарыз: O2 = O1 – V2 = 412 500 – 151 250 = 261 250. Үшінші пайыздық төлем: B3 = p·O2 = 0,1 · 261 250 = 26 125. Қарыздың үшінші төлемі: V3 = U – B3 = 192 500 – 26 125 = 166 375. Үшінші төлемнен кейінгі қалған қарыз: O3 = O2 – V3 = 261 250 – 166 375 = 94 875. Үшінші жылдан кейінгі қалған қарыз мөлшері аннуитетмөлшерінен аз екенін байқаймыз. Осы қалдықтан пайыздық ақшамөлшерін анықтамыз: B4 = p·O3 = 0,1 · 94 875 = 9 487,5. Осы қадамда қалған қарыз мөлшері толығымен қайтарылады деп есептелінеді, яғни: V4 = O3 = 94 875. Сөйтіп, басқаларынан өзгеше аннуитет мөлшерін анықтаймыз: U = V4 + B4 = 94 875 + 9 487,5 = 104 362,5. Берілген заемды өтеу жоспары 3.7–кестеде құрылған. 3.7–кесте. Заемды өтеу жоспары
Жауабы. Берілген заемды өтеу жоспары 3.7–кестеде көрсетілген. Несиені өтеудің оңтайлы нұсқасын таңдау. Коммерциялық келісім шартта қарастырылатын, қазіргікездегі төлем шамаларын салыстыратын əдіс, осы келісімшарттардың қаржылық əсерлерін талдайтын əдістердің бірі болыпесептелінеді. Сатып алушыға ең тиімді қазіргі кездегі ең кіші баға қарастырылған шарт. Барлық төлемдердің қазіргі кездегі шамаларын есептегенде бірдей пайыздық үстеме қолданылады. Алынған шамалар шартты көрсеткіштер болғанымен де, оларконтрактының артықшылығын керекті мөлшерде толық бейнелейді. Осы аталған тұжырымдарымызды тəжірибелік есеп бойыншадəлелдейік. 3.12. Берілген тапсырма бойынша құрылыс фирмасы келіскенуақытта 2000 000 долларға құрылыс объектісін бітірмекші.Берілген тапсырысты сапалы жəне уақытында бітіру үшін, құрылысфирмасы тапсырыс берушіге (заказщик) күрделі пайыздар схемасыбойынша есептеу қарастырылған, 20% пайыздық үстемемен2 000 000 доллар несие алуды жəне несиені өтеудің екі нұсқасынқарастыруды ұсынды. 1. Құрылыс фирмасы несие мөлшерінің 20% құрайтын авансарқылы төлей алады. Аванстық төлемді өткізгеннен кейін, несиеніқолданғаны үшін қарыз қалдығы бойынша пайыздық ақшаесептелінеді. Мөлшерлері бірдей постнумерандо аннуитеттерменнесиені 4 жыл бойы өтеуге болады. 2. Құрылыс фирмасына несие мөлшерінің 22% құрайтын авансарқылы төлей алады. Аванстық төлемді өткізгеннен кейін, несиеніқолданғаны үшін қарыз қалдығы бойынша пайыздық ақшаесептелінеді. Несиені өтеу үшін, осы аралықтар бойы, бірінші 6айларда пайыздық ақшалар есептелмейтін жеңілдік аралығы қарастырылған. Мөлшерлері бірдей постнумерандо аннуитеттерменнесиені 6 жыл бойы өтеуге болады. Объект құрылысын ұсынылған нұсқалармен іске асыружұмысының бағасын жəне ұсынылған нұсқалардың қайсысыжұмыс тапсырушыға тиімді екенін анықтау қажет. Шешуі. Біріншіден 1 жəне 2 нұсқа бойынша несиені өтейтін,сəйкесінше U1 жəне U2 аннуитеттерінің шамаларын анықтаймыз.Сонымен қатар сəйкесінше, льготтық аралық үшін қарапайымпайыздарды есептейтін формуланы, ал жеңілдіктері жоқаралықтарға күрделі пайыздар формуласын қолданамыз, яғни:
Егер 1–нұсқаны таңдасақ, онда құрылыстың қазіргі кездегііске асырғаннан кейінгі бағасын мына формуланы қолданып (7–шітақырыпта қарастырылған) жəне авансқа алынған ақшамен қосаесептейміз:
мұндағы a – аванспайызы. Егер 1–шінұсқақарастырылсаесептіңшартыбойынша: a =0,2 (немесе 20%), p = 0,2, A =2000000, n =4. Берілгенмəндердіформулағаорынақойып, нəтижесінде S2 = 2000000×0,2 + 829440× (1,2-1+1,2-2+1,2-3+1,2-4) = 2547088,384. Сонымен, 1–шінұсқабойыншаіскеасырылғанқұрылысобъектісініңбағасы 2 547 088,384 доллардықұрайды. Егер 2–нұсқанытаңдасақ, ондақұрылыстыңқазіргікездегібағасын 1–шінұсқабойыншақарастырылғанформуламенжəнебіріншіжылы 6 айлардапайыздықақшаларесептелмейтін жеңілдікаралығы қарастырылғанынескеріп, осығансəйкесформулағатүзетуенгізіп, нəтижесіндеаламыз:
Сонымен, 2–шінұсқабойыншаіскеасырылғанқұрылысобъектесінің бағасы 2 715 268,84 долларды құрайды. Жауабы. 1–ші нұсқа жұмыс тапсырушыға несиені өтеу үшін тиімді.
9 ТАҚЫРЫП. ҚАРЖЫЛЫҚАҒЫМДАРМОДЕЛЬДЕРІ. 3.4. А н ы қ т а м а. Қаржылық рента деп бірдей уақытаралықтары өткен сайын іске асырылатын төлемдер тіркесінатайды. 3.5. А н ы қ т а м а. Тұрақты қаржылық рента деп бірдейуақыт аралығында бірдей төлемдер өтелетін жағдайды атайды, алкерісінше жағдайда айнымалы қаржылық рента деп атайды. 3.6. А н ы қ т а м а. Егер төлемдер саны шектеулі болса, ондақаржылық рента шекті деп, ал керісінше жағдайда оны шексіз депатайды. Қаржылық ренталар күнделікті өмірде жиі кездеседі.Қаржылық рентаның қарапайым мысалы ретінде жалақыны алуғаболады. Жалақыны бастық уақытылы төлеп тұрса, онда ол тұрақтыкаржылық рента болатыны, сөзсіз. Қаржылық ренталарға зейнетақыларды, тұтынушылық несиелерді өтеу үшін жасалатынтөлемдерді, жалға алынған жəне жалданған келісімдер бойыншажасалған төлемдерді, əртүрлі қаржылық төлемдерді жəне т.б.жатқызуға болады. Ереже бойынша, ренталық сомаларпайдаланылса, пайыздық ақшалар есептелінеді. Бірінші кезекте қарапайым пайыздарды санаудықарастырайық. 3.13. Салымшы, 2008 жылдың 1–ші қаңтарынан бастап, əрбірайдың бірінші күнінде, банкке өзінің шотына 2000 доллар салады.Есеп, 6% жылдық үстемемен, пайыздық ақшалар ай сайынсаналып, қарапайым пайыздар схемасы бойынша жүргізіле-ді. Біржыл 30 күндерден тұратын 12 айлардан құралған деп есептелінеді.Салымшы шотында 2017 жылдың 31 желтоқсанында қандай сомаболады? Шешуі. Шотқа салынған ақшаның бірінші сомасына, 120айлар бойы пайыздық ақшалар есептелінеді, ол ай сайын 6% / 12=0,5% артады.Сондықтан 2017 жылдың 31 желтоқсанына дейінбірінші сома 2000 доллар мына сомаға жетеді: C1 = 2000·(1 + 0,005·120) = 3200. Шотқа түскен екінші сомаға, пайыздық ақшалар 119 айларбойы саналады да, ол 2017 жылдың 31 желтоқсанында мына сомағажетеді: C 2 = 2000·(1 + 0,005·119) = 3190. Шотқа түскен үшінші сома: C 3 = 2000·(1 + 0,005·118) = 3180 жəне т.б.с.с. Сонымен, ақырында біз кемімелі C 1, C 2, …, C 120, біріншімүшесі C 1=3200, ал айырымы (–10) тең арифметикалық прогрессияаламыз. Арифметикалық прогрессияның соңғы мүшесі: C120 = 2000·(1 + 0,005) = 2010. Арифметикалық прогрессияның мүшелерінің қосындысы:
Жауабы. 2017 жылы 31 желтоқсанда шотта 312 600 доллар болады. 3.14. Салымшы, 2008 жылдың 1–ші қаңтарынан бастап, əрбіржылдың бірінші күнінде, банкке өзінің шотына 200 000 долларсалады. Есеп, 6 % жылдық пайыздық үстемемен күрделі пайыздарсхемасы бойынша жүргізіледі. Салымшы шотында 2017 жылдың 31желтоқсанында қандай сома болады? Шешуі. Шотқа салынған ақшаның бірінші сомасына 10 жылбойы пайыздық ақшалар есептелінеді. Сондықтан 2017 жылдың 31желтоқсанына дейін бірінші сома (200 000 доллар) мына сомағажетеді: C1 = 200 000·(1 + 0,06)10 = 358 169,52. Шотқа түскен екінші сомаға, 9 жыл бойы пайыздық ақшаларсаналады да, ол 2017 жылдың 31 желтоқсанында мына сомағажетеді: C2 = 2000·(1 + 0,06)9 = 337895,78. Шотқа түскен үшінші сома: C3 = 2000·(1 + 0,06)8 = 318769,6 жəне т.б.с.с. Сонымен, ақырында біз кемімелі C 1, C 2, …, C 120, біріншімүшесі C 1=358 169,52, ал бөлімі q = 1 / 1,06= 0,9434 геометриялықпрогрессия аламыз. Геометриялық прогрессияның соңғы мүшесі: C10 = 200 000·(1 + 0,06) = 212 000. Геометриялық прогрессияның мүшелерінің қосындысы:
Жауабы. 2017 жылы 31 желтоқсанда шотта 2 794 500,3 доллар болады. 3.15. Жеке меншіктегі алма бақтың иесі бақты «шексіз» жалғаберді. Жалға алушы 2007 жылдан бастап, əрбір жылдың 1–шіқаңтарынан алма бағын жалға берушінің банктегі шотына 50 000доллар мөлшерінде аренда төлемін аударады. Банк жыл сайын алмабақтың иесінің салымына 5 % жылдық пайыздық үстемені күрделіпайыздар схемасы бойынша есептейді. Алма бағының 2007жылдың 1–ші қаңтарында сатылған құны қандай? Шешуі. 2008 жылдың 1–ші қаңтарында өтелетін екінші төлем2007 жылдың 1–ші қаңтарында өтелетін бірінші төлемменэквивалентті (7–ші тақырып). Олай болса, есеп 5 % үстемеменкүрделі пайыздар схемасы бойынша жүргізілуіне байланысты мынаформуламен екінші төлемді анықтаймыз: C2 = 50 000·(1 + 0,05)–1 = 47 619,047. Осылай талдай келе 2009 жылдың 1–ші қаңтарында өтелетін үшінші төлем: C3 = 50 000·(1 + 0,05)–2 = 45 351,473. Төртінші төлем: C4 = 50 000·(1 + 0,05)–3 = 43 191,879 жəне т.б.с.с. Сонымен, ақырында біз кемімелі C 1, C 2, C 3,.... бірінші мүшесі C1 =50 000, ал бөлімі q = 1 / 1,05= 0,9524 геометриялық прогрессияаламыз. Геометриялық прогрессияның мүшелерінің қосындысы:
алма бағының 2007 жылдың 1–ші қаңтарында сатылғанқұнын көрсетеді. Жауабы. 2007 жылы 1 қаңтарда алма бағы 1 050 420 долларға сатылған. 3.16. 3.15. есептің шарты бойынша алма бағының 2016жылдың 1–ші қаңтарында сатылған құны қандай? Шешуі. 2007 жылдың 1–ші қаңтарында өтелген 1 050 420доллар мөлшері 2016 жылдың 1–ші қаңтарында өтелетін төлемменэквивалентті (7–ші тақырып). Олай болса, есеп 5% үстемеменкүрделі пайыздар схемасы бойынша жүргізілуіне байланысты мынаформуламен 10–шы жылғы төлемді анықтаймыз: C = 1 050 420·(1 + 0,05)10 = 1 215 992,4. Ол алма бағының 2016 жылдың 1–ші қаңтарында сатылғанқұнын көрсетеді. Жауабы. 2016 жыл 1 қаңтарда алма бағы 1 215 992,4 долларғасатылады. Қаржылық рента жəне төлемдер ағымы. Қаржылық ағымдар адамның кез келген іс–əрекетініңқұрамдарына жататын жəне бөлінбейтін бір бөлігі. Саудада олартауарлар қозғалысының табыс көзін құрайды. Адамдардың мұқтаждығын қанағаттандыратын, экономикалық, қаржылық,өндірістік жəне басқа да орталарда мұндай ағымдар қызығушылықтудырады жəне осындай ортаның болуы маңызды екенінтүсіндіреді. Мұндай ағымдарға, келісілген шарт бойыншатөлемдерді бірден өтеу немесе бөліп–бөліп əртүрлі уақыт аралықтарында төлеу, банктік қарыздарды немесе коммерциялықнесиелерді бөліктерге бөліп өтеу жəне т.б.с.с. əрекеттердіжатқызады. Бұл кезде бірінен кейін бірі тіркескен қатар төлемдері,бір–бірімен шамалары бірдей, бүтін бір ағым төлемдері пайдаболады. Ағым – бір бағытта бірінен кейін бірін төлеу үрдісі. Оңтаңбалы төлемдер ақшаның түскенін, ал теріс таңбалы төлемдерақшаның төленгенін көрсетеді. Ағым бірнеше ағым мүшелерінен тұрады. Қайталану реттеріне байланысты ағымдар жүйелі немесе жүйесіз болып екіге бөлінеді. Барлық мүшелері оң таңбалы жəне олар бірдей уақытаралығында келіп түсетін болса, мұндай ағым қаржылық рента деп аталатыны (3.4-анықтама) жоғарыда келтірілді. Кейде мұндайқаржылық ағым аннуитет деп те аталады. Қаржылық рентасипатталады: – R j –рента мүшелерімен (жеке төлемдердің мөлшерімен); – t i - рента аралықтарымен (бір–бірінен кейін төленетін екіnтөлемнің уақыт аралығы); – t –рента мерзімімен (бірінші төлемнен бастап, соңғытөлемге дейінгі уақыт аралығы); – пайыздық үстемемен (ұлғайтуды есептеу немесетөлемдерді дисконттау); – соңғы төлем күнмен бірге пайыздарымен қоса барлық ағымnтөлем мүшелері, рентаның ұлғайтылған келешектегіnсомасы; – ағым төлемдерінің барлық мүшелерінің қосындысы қазіргіm(келтірілген) рента шамасы, рентаны бастапқы уақытmмезгіліне дисконттау, яғни есептік үстеме шамасынаnкішірейту. Ренталар – жыл бойы төленген рента мүшелерінің санынаnайланысты: жылдықтар жəне h – тез аралықтар (жылына h рет); пайыздарды капитализациялау ти
|

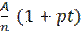 (6.1)
(6.1) (6.2)
(6.2)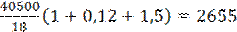
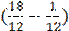 )= 3106,08 теңге.
)= 3106,08 теңге.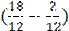 )= 3079,53 теңге.
)= 3079,53 теңге.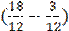 )= 3052,98 теңге
)= 3052,98 теңге
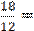 7290
7290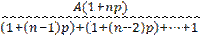 (6.4)
(6.4)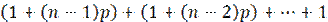 =
= 
 (6.5)
(6.5) =87500 (6.6)
=87500 (6.6) (1+pt) =
(1+pt) =  (6.7)
(6.7)